Orthogonal Range Queries
In this section we develop methods for doing orthogonal range queries in K-dimensional space as extensions of the methods for doing 1-D range queries. We will consider several standard methods. In addition, we introduce a new method of using cells coupled with a binary search.
The execution time and memory usage of tree methods and cell methods depend on the leaf size and cell size, respectively. For these methods we will examine their performance in 3-D on two test problems.
Test Problems
The records in the test problems are points in 3-D. We do an orthogonal range query around each record. The query range is a small cube.
Chair
For the chair problem, the points are vertices in the surface mesh of a chair. See the figure below for a plot of the vertices in a low resolution mesh. For the tests in this section, the mesh has 116,232 points. There is unit spacing between adjacent vertices. The query size is 8 in each dimension. The orthogonal range queries return a total of 11,150,344 records.

Points in the surface mesh of a chair. 7200 points.
Random Points
For the random points problem, the points are uniformly randomly distributed in the unit cube, ![$[0 .. 1]^3$](form_46.png) . There are 100,000 points. To test the effect of varying the leaf size or cell size, the query range will have a size of 0.1 in each dimension. For this case, the orthogonal range queries return a total of 9,358,294 records. To show how the best leaf size or cell size varies with different query ranges, we will use ranges which vary in size from 0.01 to 0.16.
. There are 100,000 points. To test the effect of varying the leaf size or cell size, the query range will have a size of 0.1 in each dimension. For this case, the orthogonal range queries return a total of 9,358,294 records. To show how the best leaf size or cell size varies with different query ranges, we will use ranges which vary in size from 0.01 to 0.16.
Sequential Scan
The simplest approach to the orthogonal range query problem is to examine each record and test if it is in the range. Below is the sequential scan algorithm.
ORQ_sequential_scan(file, range) included_records =for record in file: if record
range: included_records += record return included_records
The sequential scan algorithm is implemented by storing pointers to the records in an array or list. Thus the preprocessing time and storage complexity is 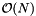 . Since each record is examined once during an orthogonal range query, the complexity is
. Since each record is examined once during an orthogonal range query, the complexity is 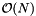 . The performance of the sequential scan algorithm is acceptable only if the file is small. However, the sequential scan (or a modification of it) is used in all of the orthogonal range query algorithms to be presented.
. The performance of the sequential scan algorithm is acceptable only if the file is small. However, the sequential scan (or a modification of it) is used in all of the orthogonal range query algorithms to be presented.
![\[ \mathrm{Preprocess} = \mathcal{O}(N), \quad \mathrm{Reprocess} = 0, \quad \mathrm{Storage} = \mathcal{O}(N), \quad \mathrm{Query} = \mathcal{O}(N) \]](form_10.png)
Projection
We extend the idea of a binary search on sorted data presented previously to higher dimensions. We simply sort the records in each dimension. Let sorted[k] be an array of pointers to the records, sorted in the 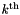 dimension. This is called the projection method because the records are successively projected onto each coordinate axis before each sort. Doing a range query in one coordinate direction gives us all the records that lie in a slice of the domain. This is depicted below in three dimensions. The orthogonal range along with the slices obtained by doing range queries in each direction are shown. To perform an orthogonal range query, we determine the number of records in each slice by finding the beginning and end of the slice with binary searches. Then we choose the slice with the fewest records and perform the sequential scan on those records.
dimension. This is called the projection method because the records are successively projected onto each coordinate axis before each sort. Doing a range query in one coordinate direction gives us all the records that lie in a slice of the domain. This is depicted below in three dimensions. The orthogonal range along with the slices obtained by doing range queries in each direction are shown. To perform an orthogonal range query, we determine the number of records in each slice by finding the beginning and end of the slice with binary searches. Then we choose the slice with the fewest records and perform the sequential scan on those records.

The projection method. The query range is the intersection of the three slices.
ORQ_projection(range): // Do binary searches in each direction to find the size of the slices. for k[0..K): slice[k].begin = binary_search_lower_bound(sorted[k].begin, sorted[k].end, range.min[k]) slice[k].end = binary_search_upper_bound(sorted[k].begin, sorted[k].end, range.max[k]) smallest_slice = slice with the fewest elements. return ORQ_sequential_scan(smallest_slice, range)
The projection method requires storing K arrays of pointers to the records so the storage requirement is 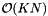 . Preprocessing is comprised of sorting in each direction and so has complexity
. Preprocessing is comprised of sorting in each direction and so has complexity 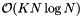 . Reprocessing can be accomplished by insertion sorting the K arrays of pointers to records. (See Introduction to Algorithms, Second Edition.) Thus it has complexity
. Reprocessing can be accomplished by insertion sorting the K arrays of pointers to records. (See Introduction to Algorithms, Second Edition.) Thus it has complexity 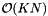 .
.
The orthogonal range query is comprised of two steps: 1) Determine the K slices with 2K binary searches on the the N records at a cost of 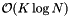 . 2) Perform a sequential scan on the smallest slice. Thus the computational complexity for a query is
. 2) Perform a sequential scan on the smallest slice. Thus the computational complexity for a query is 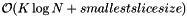 . Typically the number of records in the smallest slice is much greater than
. Typically the number of records in the smallest slice is much greater than 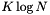 , so the sequential scan is more costly than the binary searches. Consider the case that the records are uniformly distributed in
, so the sequential scan is more costly than the binary searches. Consider the case that the records are uniformly distributed in ![$[0..1]^K$](form_53.png) . The expected distance between adjacent records is of the order
. The expected distance between adjacent records is of the order 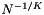 . Suppose that the query range is small and has length
. Suppose that the query range is small and has length 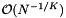 in each dimension. Then the volume of any of the slices is of the order
in each dimension. Then the volume of any of the slices is of the order 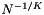 and thus contains
and thus contains 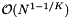 records. The sequential scan on these records will be more costly than the binary searches. Below we give the expected cost for this case. In general, the projection method has acceptable performance only if the total number of records is small or if the number of records in some slice is small.
records. The sequential scan on these records will be more costly than the binary searches. Below we give the expected cost for this case. In general, the projection method has acceptable performance only if the total number of records is small or if the number of records in some slice is small.
![\[ \mathrm{Preprocess} = \mathcal{O}(K N \log N), \quad \mathrm{Reprocess} = \mathcal{O}(K N), \quad \mathrm{Storage} = \mathcal{O}(K N), \]](form_57.png)
![\[ \mathrm{Query} = \mathcal{O}(K \log N + \text{smallest slice size}), \mathrm{AverageQuery} = \mathcal{O}\left( K \log N + N^{1 - 1 / K} \right) \]](form_58.png)
Point-in-Box Method
A modification of the projection method was developed by J. W. Swegle. (See A parallel contact detection algorithm for transient solid dynamics simulations using PRONTO3D and A general-purpose contact detection algorithm for nonlinear structural analysis codes where they apply the method to the contact detection problem.) In addition to sorting the records in each coordinate direction, the rank of each record is stored for each direction. When iterating through the records in the smallest slice the rank arrays are used so that one can compare the rank of keys instead of the keys themselves. This allows one to do integer comparisons instead of floating point comparisons. On some architectures, like a Cray Y-MP, this modification will significantly improve performance, on others, like most x86 processors, it has little effect. Also, during the sequential scan step, the records are not accessed, only their ranks are compared. This improves the performance of the sequential scan.
The projection method requires K arrays of pointers to records. For the Point-in-Box method, there is a single array of pointers to the records. There are K arrays of pointers to the record pointers which sort the records in each coordinate direction. Finally there are K arrays of integers which hold the rank of each record in the given coordinate. Thus the storage requirement is 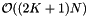 . The point-in-box method has the same computational complexity as the projection method, but has a higher storage overhead. Below are the methods for initializing the arrays and performing an orthogonal range query.
. The point-in-box method has the same computational complexity as the projection method, but has a higher storage overhead. Below are the methods for initializing the arrays and performing an orthogonal range query.
initialize(): // Initialize the vectors of sorted pointers. for i[0..num_records): for k
[0..K): sorted[k][i] = record_pointers.begin + i // Sort in each direction. for k
[0..K): sort_by_coordinate(sorted[k].begin, sorted[k].end, k) // Make the rank vectors. for i
[0..num_records): for k
[0..K): rank[k][sorted[k][i] - record_pointers.begin] = i return
ORQ_point_in_box(range): // Do binary searches in each direction to find the size of the slices. for k[0..K): slice[k].begin = binary_search_lower_bound(sorted[k].begin, sorted[k].end, range.min[k]) slice[k].end = binary_search_upper_bound(sorted[k].begin, sorted[k].end, range.max[k]) rank_range.min[k] = slice[k].begin - sorted[k].begin rank_range.max[k] = slice[k].end - sorted[k].end smallest_slice = slice with the fewest elements. // Do a sequential scan on the smallest slice. included_records =
for ptr
[smallest_slice.begin .. smallest_slice.end): for k
[0..K): record_rank[k] = rank[k][*ptr - record_pointers.begin] if record_rank
rank_range: included_records += **ptr return included_records
![\[ \mathrm{Preprocess} = \mathcal{O}(K N \log N), \quad \mathrm{Reprocess} = \mathcal{O}(K N), \quad \mathrm{Storage} = \mathcal{O}((2 K + 1) N), \]](form_60.png)
![\[ \mathrm{Query} = \mathcal{O}(K \log N + \mathrm{smallest slice size}), \quad \mathrm{AverageQuery} = \mathcal{O}\left( K \log N + N^{1 - 1 / K} \right) \]](form_61.png)
Kd-Trees
We generalize the trees with median splitting presented previously to higher dimensions. Now instead of a single median, there are K medians, one for each coordinate. We split in the key with the largest spread. (We could use the distance from the minimum to maximum keys or some other measure of how spread out the records are.) The records are recursively split by choosing a key (direction), and putting the records less than the median in the left branch and the other records in the right branch. The recursion stops when there are no more than leaf_size records. These records are then stored in a leaf. The figure below depicts a kd-tree in 2-D with a leaf size of unity. Horizontal and vertical lines are drawn through the medians to show the successive splitting. A kd-tree divides a domain into hyper-rectangles. Note that the depth of the kd-tree is determined by the number of records alone and is 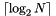 .
.

A kd-tree in 2-D.
Below is the function construct(), which constructs the kd-tree and returns its root. Leaves in the tree simply store records. Branches in the tree must store the dimension with the largest spread, split_dimension, the median value in that dimension, discriminator, and the left and right sub-trees.
construct(file):
if file.size > leaf_size:
return construct_branch(file)
else:
return construct_leaf(file)
construct_branch(file):
branch.split_dimension = dimension with largest spread
branch.discriminator = median key value in split_dimension
left_file = records with key < discriminator in split_dimension
if left_file.size > leaf_size:
branch.left = construct_branch(left_file)
else:
branch.left = construct_leaf(left_file)
right_file = records with key 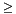 discriminator in split_dimension
if right_file.size > leaf_size:
branch.right = construct_branch(right_file)
else:
branch.right = construct_leaf(right_file)
return branch
discriminator in split_dimension
if right_file.size > leaf_size:
branch.right = construct_branch(right_file)
else:
branch.right = construct_leaf(right_file)
return branch
construct_leaf(file): leaf.records = file return leaf
We define the orthogonal range query recursively. When we are at a branch in the tree, we check if the domains of the left and right sub-trees intersect the query range. We can do this by examining the discriminator. If the discriminator is less than the lower bound of the query range (in the splitting dimension), then only the right tree intersects the query range so we return the ORQ on that tree. If the discriminator is greater than the upper bound of the query range, then only the left tree intersects the query range so we return the ORQ on the left tree. Otherwise we return the union of the ORQ's on the left and right trees. When we reach a leaf in the tree, we use the sequential scan algorithm to check the records.
ORQ_KDTree(node, range):
if node is a leaf:
return ORQ_sequential_scan(node.records, range)
else:
if node.discriminator < range.min[node.split_dimension]:
return ORQ_KDTree(node.right, range)
else if node.discriminator > range.max[node.split_dimension]:
return ORQ_KDTree(node.left, range)
else:
return (ORQ_KDTree(node.left, range) + ORQ_KDTree(node.right, range))
Note that with the above implementation of ORQ's, every record that is returned is checked for inclusion in the query range with the sequential scan algorithm. Thus the kd-tree identifies the records that might be in the query range and then these records are checked with the brute force algorithm. If the query range contains most of the records, then we expect that the kd-tree will perform no better than the sequential scan algorithm. Below we give an algorithm that has better performance for large queries. As we traverse the tree, we keep track of the domain containing the records in the current sub-tree. If the current domain is a subset of the query range, then we can simply report the records and avoid checking them with a sequential scan. Note that this modification does not affect the computational complexity of the algorithm but it will affect performance. The additional work to maintain the domain will increase the query time for small queries (small meaning that the number of records returned is not much greater than the leaf size). However, this additional bookkeeping will pay off when the query range spans many leaves.
ORQ_KDTree_domain(node, range, domain):
if node is a leaf:
if domain 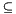 range:
return node.records
else:
return ORQ_sequential_scan(node.records, range)
else:
if node.discriminator
range:
return node.records
else:
return ORQ_sequential_scan(node.records, range)
else:
if node.discriminator 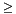 range.min[node.split_dimension]:
domain_max = domain.max[node.split_dimension]
domain.max[node.split_dimension] = node.discriminator
if domain
range.min[node.split_dimension]:
domain_max = domain.max[node.split_dimension]
domain.max[node.split_dimension] = node.discriminator
if domain 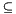 range:
included_records += report(node.left)
else:
included_records += ORQ_KDTree(node.left, domain, range)
domain.max[node.split_dimension] = domain_max
if node.discriminator
range:
included_records += report(node.left)
else:
included_records += ORQ_KDTree(node.left, domain, range)
domain.max[node.split_dimension] = domain_max
if node.discriminator 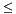 range.max[node.split_dimension]:
domain_min = domain.min[node.split_dimension]
domain.min[node.split_dimension] = node.discriminator
if domain
range.max[node.split_dimension]:
domain_min = domain.min[node.split_dimension]
domain.min[node.split_dimension] = node.discriminator
if domain 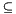 range:
included_records += report(node.right)
else:
included_records += ORQ_KDTree(node.right, domain, range)
domain.min[node.split_dimension] = domain_min
return included_records
range:
included_records += report(node.right)
else:
included_records += ORQ_KDTree(node.right, domain, range)
domain.min[node.split_dimension] = domain_min
return included_records
The worst-case query time for kd-trees is 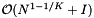 , which is not very encouraging. (See Data Structures for Range Searching.) However, if the query range is nearly cubical and contains few elements the average case performance is much better:
, which is not very encouraging. (See Data Structures for Range Searching.) However, if the query range is nearly cubical and contains few elements the average case performance is much better:
![\[ \mathrm{Preprocess} = \mathcal{O}(N \log N), \quad \mathrm{Reprocess} = \mathcal{O}(N \log N), \quad \mathrm{Storage} = \mathcal{O}(N), \]](form_64.png)
![\[ \mathrm{Query} = \mathcal{O}\left( N^{1 - 1 / k} + I \right), \quad \mathrm{AverageQuery} = \mathcal{O}(\log N + I) \]](form_65.png)
The figures below show the execution times and storage requirements for the chair problem. The best execution times are obtained for leaf sizes of 4 or 8. There is a moderately high memory overhead for small leaf sizes. For the random points problem, a leaf size of 8 gives the best performance and has a modest memory overhead.

The effect of leaf size on the execution time for the kd-tree and the chair problem.

The effect of leaf size on the memory usage for the kd-tree and the chair problem.

The effect of leaf size on the execution time for the kd-tree and the random points problem.

The effect of leaf size on the memory usage for the kd-tree and the random points problem.
In the figure below we show the best leaf size versus the average number of records in a query for the random points problem. We see that the best leaf size is correlated to the number of records in a query. For small query sizes, the best leaf size is on the order of the number of records in a query. For larger queries, it is best to choose a larger leaf size. However, the best leaf size is much smaller than the number of records in a query. This leaf size balances the costs of accessing leaves and testing records for inclusion in the range. It reflects that the cost of accessing many leaves is amortized by the structure of the tree.

The best leaf size as a function of records per query for the kd-tree and the random points problem.

The ratio of the number of records per query and the leaf size.
Quadtrees and Octrees
We can also generalize the trees with midpoint splitting presented previously to higher dimensions. Now instead of splitting an interval in two, we split a K-dimensional domain into 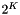 equal size hyper-rectangles. Each non-leaf node of the tree has
equal size hyper-rectangles. Each non-leaf node of the tree has 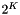 branches. We recursively split the domain until there are no more than leaf_size records, which we store at a leaf. In 2-D these trees are called quadtrees, in 3-D they are octrees. The figure below depicts a quadtree. Note that the depth of these trees depends on the distribution of records. If some records are very close, the tree could be very deep.
branches. We recursively split the domain until there are no more than leaf_size records, which we store at a leaf. In 2-D these trees are called quadtrees, in 3-D they are octrees. The figure below depicts a quadtree. Note that the depth of these trees depends on the distribution of records. If some records are very close, the tree could be very deep.

A quadtree in 2-D.
Let D be the depth of the octree. The worst-case query time is as bad as sequential scan, but in practice the octree has much better performance.
![\[ \mathrm{Preprocess} = \mathcal{O}((D + 1) N), \quad \mathrm{Storage} = \mathcal{O}((D + 1) N), \]](form_67.png)
![\[ \mathrm{Query} = \mathcal{O}\left( N + I \right) \quad \mathrm{AverageQuery} = \mathcal{O}\left( \log N + I \right) \]](form_68.png)
The figures below show the execution times and storage requirements for the chair problem. The best execution times are obtained for a leaf size of 16. There is a high memory overhead for small leaf sizes. For the random points problem, leaf sizes of 8 and 16 give the best performance. The execution time is moderately sensitive to the leaf size. Compared with the kd-tree, the octree's memory usage is higher and more sensitive to the leaf size.

The effect of leaf size on the execution time for the octree and the chair problem.

The effect of leaf size on the memory usage for the octree and the chair problem.

The effect of leaf size on the execution time for the octree and the random points problem.

The effect of leaf size on the memory usage for the octree and the random points problem.
In the figure below we show the best leaf size versus the average number of records in a query for the random points problem. We see that the best leaf size is correlated to the number of records in a query. The results are similar to those for a kd-tree, but for octrees the best leaf size is a little larger.

The best leaf size as a function of records per query for the octree for the random points problem.

The ratio of the number of records per query and the leaf size.
Cells
The cell method presented for range queries is easily generalized to higher dimensions. (See Data Structures for Range Searching.) Consider an array of cells that spans the domain containing the records. Each cell spans a rectilinear domain of the same size and contains a list or an array of pointers to the records in the cell. The figure below shows a depiction of a 2-D cell array (also called a bucket array).
We cell sort the records by converting their multikeys to cell indices. Let the cell array data structure have the attribute min which returns the minimum multikey in the domain and the attribute delta which returns the size of a cell. Below are the functions for this initialization of the cell data structure.
multikey_to_cell_index(cells, multikey): for k[0 .. K): index[k] =
(multikey[k] - cells.min[k]) / cells.delta[k]
return index
cell_sort(cells, file):
for record in file:
cells[multikey_to_cell_index(cells, record.multikey)] += record

First we depict a 2-D cell array. The 8 by 8 array of cells contains records depicted as points. Next we show an orthogonal range query. The query range is shown as a rectangle with thick lines. There are eight boundary cells and one interior cell.
An orthogonal range query consists of accessing cells and testing records for inclusion in the range. The query range partially overlaps boundary cells and completely overlaps interior cells. See the figure above. For the boundary cells we must test for inclusion in the range; for interior cells we don't. Below is the orthogonal range query algorithm.
ORQ_cell(cells, range): included_records =for each boundary_cell: for record in boundary_cell: if record
range: included_records += record for each interior_cell: for record in interior_cell: included_records += record return included_records
The query performance depends on the size of the cells and the query range. If the cells are too large, the boundary cells will likely contain many records which are not in the query range. We will waste time doing inclusion tests on records that are not close to the range. If the cells are too small, we will spend a lot of time accessing cells. The cell method is particularly suited to problems in which the query ranges are approximately the same size. Then the cell size can be chosen to give good performance. Let M be the total number of cells. Let J be the number of cells which overlap the query range and 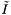 be the number of records in the overlapping cells. Suppose that the cells are no larger than the query range and that both are roughly cubical. Let R be the ratio of the length of a query range to the length of a cell in a given coordinate. In this case we expect
be the number of records in the overlapping cells. Suppose that the cells are no larger than the query range and that both are roughly cubical. Let R be the ratio of the length of a query range to the length of a cell in a given coordinate. In this case we expect 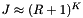 . The number of records in these cells will be about
. The number of records in these cells will be about 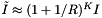 , where I is the number of records in the query range. Let AverageQuery be the expected computational complexity for this case.
, where I is the number of records in the query range. Let AverageQuery be the expected computational complexity for this case.
![\[ \mathrm{Preprocess} = \mathcal{O}(M + N), \quad \mathrm{Reprocess} = \mathcal{O}(M + N), \quad \mathrm{Storage} = \mathcal{O}(M + N), \]](form_71.png)
![\[ \mathrm{Query} = \mathcal{O}(J + \tilde{I}), \quad \mathrm{AverageQuery} = \mathcal{O}\left( (R + 1)^K + (1 + 1/R)^K I \right) \]](form_72.png)
The figure below shows the execution times and storage requirements for the chair problem. The best execution times are obtained when the ratio of cell length to query range length, R, is between 1/4 and 1/2. There is a large storage overhead for 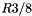 . For the random points problem, the best execution times are obtained when R is between 1/5 and 1/2. There is a large storage overhead for
. For the random points problem, the best execution times are obtained when R is between 1/5 and 1/2. There is a large storage overhead for 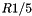 .
.

The effect of leaf size on the execution time for the cell array and the chair problem.

The effect of leaf size on the memory usage for the cell array and the chair problem.

The effect of leaf size on the execution time for the cell array and the random points problem.

The effect of leaf size on the memory usage for the cell array and the random points problem.
In the figure below we show the best cell size versus the query range size for the random points problem. We see that the best cell size is correlated to the query size. For small query sizes which return only a few records, the best cell size is a little larger than the query size. The ratio of best cell size to query size decreases with increasing query size.

The best cell size versus the query range size for the cell array on the random points problem.

The ratio of the cell size to the query range size.

The average number of records in a cell versus the average number of records returned by an orthogonal range query as a ratio.
Sparse Cells
Consider the cell method presented above. If the cell size and distribution of records is such that many of the cells are empty then the storage requirement for the cells may exceed that of the records. Also, the computational cost of accessing cells may dominate the orthogonal range query. In such cases it may be advantageous to use a sparse cell data structure in which only non-empty cells are stored and use hashing to access cells.
As an example, one could use a sparse array data structure. The figure below depicts a cell array that is sparse in the x coordinate. For cell arrays that are sparse in one coordinate, we can access a cell by indexing an array and then performing a binary search in the sparse direction. The orthogonal range query algorithm is essentially the same as that for the dense cell array.

A sparse cell array in 2-D. The array is sparse in the x coordinate. Only the non-empty cells are stored.
As with dense cell arrays, the query performance depends on the size of the cells and the query range. The same results carry over. However, accessing a cell is more expensive because of the binary search in the sparse direction. One would choose a sparse cell method when the memory overhead of the dense cell method is prohibitive. Let M be the number of cells used with the dense cell method. The sparse cell method has an array of sparse cell data structures. The array spans K - 1 dimensions and thus has size 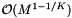 . The binary searches are performed on the sparse cell data structures. The total number of non-empty cells is bounded by N. Thus the storage requirement is
. The binary searches are performed on the sparse cell data structures. The total number of non-empty cells is bounded by N. Thus the storage requirement is 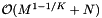 . The data structure is built by cell sorting the records. Thus the preprocessing and reprocessing times are
. The data structure is built by cell sorting the records. Thus the preprocessing and reprocessing times are 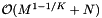 .
.
Let J be the number of non-empty cells which overlap the query range and 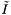 be the number of records in the overlapping cells. There will be at most J binary searches to access the cells. There are
be the number of records in the overlapping cells. There will be at most J binary searches to access the cells. There are 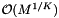 cells in the sparse direction. Thus the worst-case computational cost of an orthogonal range query is
cells in the sparse direction. Thus the worst-case computational cost of an orthogonal range query is 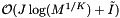 . Next we determine the expected cost of a query. Suppose that the cells are no larger than the query range and that both are roughly cubical. Let R be the ratio of the length of a query range to the length of a cell in a given coordinate. In this case
. Next we determine the expected cost of a query. Suppose that the cells are no larger than the query range and that both are roughly cubical. Let R be the ratio of the length of a query range to the length of a cell in a given coordinate. In this case 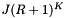 . We will have to perform about
. We will have to perform about 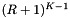 binary searches to access these cells. Each binary search will be performed on no more than
binary searches to access these cells. Each binary search will be performed on no more than 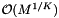 cells. Thus the cost of the binary searches is
cells. Thus the cost of the binary searches is 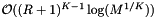 . Excluding the binary searches, the cost of accessing cells is
. Excluding the binary searches, the cost of accessing cells is 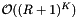 . The number of records in the overlapping cells will be about
. The number of records in the overlapping cells will be about 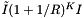 , where I is the number of records in the query range. For the interior cells, records are simply returned. For the boundary cells, which partially overlap the query range, the records must be tested for inclusion. These operations add a cost of
, where I is the number of records in the query range. For the interior cells, records are simply returned. For the boundary cells, which partially overlap the query range, the records must be tested for inclusion. These operations add a cost of 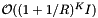 :
:
![\[ \mathrm{Preprocess} = \mathcal{O}(M^{1 - 1/K} + N), \quad \mathrm{Reprocess} = \mathcal{O}(M^{1 - 1/K} + N), \]](form_85.png)
![\[ \mathrm{Storage} = \mathcal{O}(M^{1 - 1/K} + N), \quad \mathrm{Query} = \mathcal{O}(J \log(M) / K + \tilde{I}), \]](form_86.png)
![\[ \mathrm{AverageQuery} = \mathcal{O}\left( (R + 1)^{K - 1} \log(M) / K + (R + 1)^K + (1 + 1/R)^K I \right) \]](form_87.png)
The figure below shows the execution times and storage requirements for the chair problem. Again the best execution times are obtained when R is between 1/4 and 1/2. The performance of the sparse cell arrays is very close to that of dense cell arrays. The execution times are a little higher than those for dense cell arrays for medium to large cell sizes. This reflects the overhead of the binary search to access cells. The execution times are lower than those for dense cell arrays for small cell sizes. This is due to removing the overhead of accessing empty cells.

The effect of leaf size on the performance of the sparse cell array for the chair problem. The plot shows the execution time in seconds versus R. The performance of the dense cell array is shown for comparison.

The effect of leaf size on the performance of the sparse cell array for the chair problem. The plot shows the memory usage in megabytes versus R. The performance of the dense cell array is shown for comparison.
The figure below shows the execution times and storage requirements for the random points problem. The execution times are very close to those for the dense cell array.

The effect of leaf size on the performance of the sparse cell array for the random points problem. The plot shows the execution time in seconds versus R. The performance of the dense cell array is shown for comparison.

The effect of leaf size on the performance of the sparse cell array for the random points problem. The plot shows the memory usage in megabytes versus R. The performance of the dense cell array is shown for comparison.
In the figure below we show the best cell size versus the query range size for the random points problem. We see that the best cell size is correlated to the query size. The results are very similar to those for dense cell arrays. For sparse cell arrays, the best cell size is slightly larger due to the higher overhead of accessing a cell.

The best cell size versus the query range size for the sparse cell array on the random points problem.

The ratio of the cell size to the query range size.

The average number of records in a cell versus the average number of records returned by an orthogonal range query as a ratio.
Cells Coupled with a Binary Search
One can couple the cell method with other search data structures. For instance, one could sort the records in each of the cells or store those records in a search tree. Most such combinations of data structures do not offer any advantages. However, there are some that do. Based on the success of the sparse cell method, we couple a binary search to a cell array. For the sparse cell method previously presented, there is a dense cell array which spans K - 1 dimensions and a sparse cell structure in the final dimension. Instead of storing sparse cells in the final dimension, we store records sorted in that direction. We can access a record with array indexing in the first K - 1 dimensions and a binary search in the final dimension. See the figure below for a depiction of a cell array with binary searching.

First we depict a cell array with binary search in 2-D. There are 8 cells which contain records sorted in the x direction. Next we show an orthogonal range query. The query range is shown as a rectangle with thick lines. There are three overlapping cells.
We construct the data structure by cell sorting the records and then sorting the records within each cell. Let the data structure have the attribute min which returns the minimum multikey in the domain and the attribute delta which returns the size of a cell. Let cells be the cell array. Below is the method for constructing the data structure.
multikey_to_cell_index(multikey): for k[0..K-1): index[k]
(multikey[k] - min[k]) / delta[k]
return index
construct(file):
for record in file:
cells[multikey_to_cell_index(record.multikey)] += record
for cell in cells:
sort_by_last_key(cell)
return
The orthogonal range query consists of accessing cells that overlap the domain and then doing a binary search followed by a sequential scan on the sorted records in each of these cells. Below is the orthogonal range query method.
ORQ_cell_binary_search(range): included_records =min_index = multikey_to_index(range.min) max_index = multikey_to_index(range.max) for index in [min_index..max_index]: iter = binary_search_lower_bound(cells[index].begin, cells[index].end, range.min[K-1]) while (*iter).multikey[K-1]
range.max[K-1]: if *iter
range: included_records += iter return included_records
As with sparse cell arrays, the query performance depends on the size of the cells and the query range. The same results carry over. The only differences are that the binary search on records is more costly than the search on cells, but we do not have the computational cost of accessing cells in the sparse data structure or the storage overhead of those cells. Let M be the number of cells used with the dense cell method. The cell with binary search method has an array of cells which contain sorted records. This array spans K - 1 dimensions and thus has size 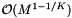 . Thus the storage requirement is
. Thus the storage requirement is 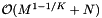 . The data structure is built by cell sorting the records and then sorting the records within each cell. We will assume that the records are approximately uniformly distributed. Thus each cell contains
. The data structure is built by cell sorting the records and then sorting the records within each cell. We will assume that the records are approximately uniformly distributed. Thus each cell contains 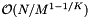 records. Thus each sort of the records in a cell costs
records. Thus each sort of the records in a cell costs 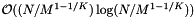 . The preprocessing time is
. The preprocessing time is 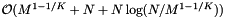 . We can use insertion sort for reprocessing, so its cost is
. We can use insertion sort for reprocessing, so its cost is 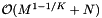 .
.
Let J be the number of cells which overlap the query range and 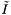 be the number of records which are reported or checked for inclusion in the overlapping cells. There will be J binary searches to find the starting record in each cell. Thus the worst-case computational complexity of an orthogonal range query is
be the number of records which are reported or checked for inclusion in the overlapping cells. There will be J binary searches to find the starting record in each cell. Thus the worst-case computational complexity of an orthogonal range query is 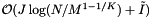 . Next we determine the expected cost of a query. Suppose that the cells are no larger than the query range and that both are roughly cubical (except in the binary search direction). Let R be the ratio of the length of a query range to the length of a cell in a given coordinate. In this case
. Next we determine the expected cost of a query. Suppose that the cells are no larger than the query range and that both are roughly cubical (except in the binary search direction). Let R be the ratio of the length of a query range to the length of a cell in a given coordinate. In this case 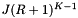 . Thus the cost of the binary searches is
. Thus the cost of the binary searches is 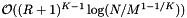 . The number of records in the overlapping cells that are checked for inclusion is about
. The number of records in the overlapping cells that are checked for inclusion is about 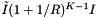 , where I is the number of records in the query range. These operations add a cost of
, where I is the number of records in the query range. These operations add a cost of 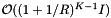 :
:
![\[ \mathrm{Preprocess} = \mathcal{O}( M^{1 - 1/K} + N + N \log(N / M^{1 - 1/K}) ), \quad \mathrm{Reprocess} = \mathcal{O}(M^{1 - 1/K} + N), \]](form_97.png)
![\[ \mathrm{Storage} = \mathcal{O}(M^{1 - 1/K} + N), \quad \mathrm{Query} = \mathcal{O}(J \log(N / M^{1 - 1/K}) + \tilde{I}), \]](form_98.png)
![\[ \mathrm{AverageQuery} = \mathcal{O}\left( (R + 1)^{K - 1} \log \left( N / M^{1 - 1/K} \right) + (1 + 1/R)^{K-1} I \right) \]](form_99.png)
The figures below show the execution times and storage requirements for the chair problem. Like the sparse cell array, the best execution times are obtained when R is between 1/4 and 1/2. The performance of the cell array coupled with a binary search is comparable to that of the sparse cell array. However, it is less sensitive to the size of the cells. Also, compared to sparse cell arrays, there is less memory overhead for small cells.

The effect of leaf size on the performance of the cell array coupled with binary searches for the chair problem. The plot shows the execution time in seconds versus R. The performance of the sparse cell array is shown for comparison.

The effect of leaf size on the performance of the cell array coupled with binary searches for the chair problem. The plot shows the memory usage in megabytes versus R. The performance of the sparse cell array is shown for comparison.
The figures below show the execution times and storage requirements for the random points problem. The execution times are better than those for the sparse cell array and are less dependent on the cell size. Again, there is less memory overhead for small cells.

The effect of leaf size on the performance of the cell array coupled with binary searches for the random points problem. The plot shows the execution time in seconds versus R. The performance of the sparse cell array is shown for comparison.

The effect of leaf size on the performance of the cell array coupled with binary searches for the random points problem. The plot shows the memory usage in megabytes versus R. The performance of the sparse cell array is shown for comparison.
In the figures below we show the best cell size versus the query range size for the random points problem. Surprisingly, we see that the best cell size for this problem is not correlated to the query size.

The best cell size versus the query range size for the cell array coupled with binary searches on the random points problem.

The ratio of the cell size to the query range size.
Generated on Thu Jun 30 02:14:58 2016 for Computational Geometry Package by
 1.6.3
1.6.3