Range Queries
As a stepping stone to orthogonal range queries in K-dimensional space, we consider the problem of 1-D range queries. We will analyze the methods for doing range queries and see which ideas carry over well to higher dimensions. Consider a file of N records. Some of the methods will require only that the records are comparable. Other methods will require that the records can be mapped to numbers so that we can use arithmetic methods to divide or hash them. In this case, let the records lie in the interval ![$[\alpha .. \beta]$](form_6.png) . We wish to do a range query for the interval
. We wish to do a range query for the interval ![$[a .. b]$](form_7.png) . Let there be I records in the query range.
. Let there be I records in the query range.
We introduce the following notations for the complexity of the algorithms.
- Preprocess(N) denotes the preprocessing time to build the data structures.
- Reprocess(N) denotes the reprocessing time. That is if the records change by small amounts, Reprocess(N) is the time to rebuild or repair the data structures.
- Storage(N) denotes the storage required by the data structures.
- Query(N, I) is the time required for a range query if there are I records in the query range. For some methods, Query() will depend upon additional parameters.
- For some data structures, the average case performance is much better than the worst-case complexity. Let AverageQuery(N,I) denote the average case performance.
Sequential Scan
The simplest approach to the range query problem is to examine each record and test if it is in the range. Below is the sequential scan algorithm. See Data Structures for Range Searching. (Functions for performing range queries will have the RQ prefix.)
RQ_sequential_scan(file, range): included_records =for record in file: if record
range: included_records += record return included_records
The algorithm has the advantage that it is trivial to implement and trivial to adapt to higher dimensions and dynamic problems. However, the performance is acceptable only if the file is small or most of the records lie in the query range.
![\[ \mathrm{Preprocess} = \mathcal{O}(N), \quad \mathrm{Reprocess} = 0, \quad \mathrm{Storage} = \mathcal{O}(N), \quad \mathrm{Query} = \mathcal{O}(N) \]](form_10.png)
Binary Search on Sorted Data
If the records are sorted, then we can find any given record with a binary search at a cost of 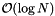 . To do a range query for the interval
. To do a range query for the interval ![$[a .. b]$](form_7.png) , we use a binary search to find the first record x that satisfies
, we use a binary search to find the first record x that satisfies 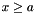 . Then we collect records x in order while
. Then we collect records x in order while 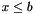 . Alternatively, we could also do a binary search to find the last record in the interval. Then we could iterate from the first included record to the last without checking the condition
. Alternatively, we could also do a binary search to find the last record in the interval. Then we could iterate from the first included record to the last without checking the condition 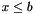 . Either way, the computational complexity of the range query is
. Either way, the computational complexity of the range query is 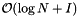 .
.
To find the first record in the range we use binary_search_lower_bound(). begin and end are random access iterators to the sorted records. The function returns the first iterator whose key is greater than or equal to value. (Note that this binary search is implemented in the C++ STL function std::lower_bound(). See Generic programming and the STL: using and extending the C++ Standard Template Library.)
binary_search_lower_bound(begin, end, value):
if begin == end:
return end
middle = (begin + end) / 2
if *middle < value:
return binary_search_lower_bound(middle + 1, end, value)
else:
return binary_search_lower_bound(begin, middle, value)
To find the last record in the range we use binary_search_upper_bound(), which returns the last iterator whose key is less than or equal to value. (This binary search is implemented in the C++ STL function std::upper_bound().)
binary_search_upper_bound(begin, end, value):
if begin == end:
return end
middle = (begin + end) / 2
if value < *middle:
return binary_search_lower_bound(begin, middle, value)
else:
return binary_search_lower_bound(middle + 1, end, value)
Below are the two methods of performing a range query with a binary search on sorted records. If the number of records in the interval is small, specifically 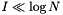 then RQ_binary_search_single will be more efficient. RQ_binary_search_double has better performance when there are many records in the query range.
then RQ_binary_search_single will be more efficient. RQ_binary_search_double has better performance when there are many records in the query range.
RQ_binary_search_single(sorted_records, range = [a..b]): included_records =iter = binary_search_lower_bound(sorted_records.begin, sorted_records.end, a) while *iter
b: included_records += iter ++iter return included_records
RQ_binary_search_double(sorted_records, range = [a..b]): included_records =begin = binary_search_lower_bound(sorted_records.begin, sorted_records.end, a) end = binary_search_upper_bound(sorted_records.begin, sorted_records.end, b) for iter in [begin..end): included_records += iter return included_records
The preprocessing time is 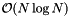 because the records must be sorted. The reprocessing time is
because the records must be sorted. The reprocessing time is 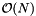 , because a nearly sorted sequence can be sorted in linear time with an insertion sort. (See Introduction to Algorithms, Second Edition.) The storage requirement is linear because the data structure is simply an array of pointers to the records.
, because a nearly sorted sequence can be sorted in linear time with an insertion sort. (See Introduction to Algorithms, Second Edition.) The storage requirement is linear because the data structure is simply an array of pointers to the records.
![\[ \mathrm{Preprocess} = \mathcal{O}(N \log N), \quad \mathrm{Reprocess} = \mathcal{O}(N), \]](form_19.png)
![\[ \mathrm{Storage} = \mathcal{O}(N), \quad \mathrm{Query} = \mathcal{O}(\log N + I) \]](form_20.png)
Trees
The records in the file can be stored in a binary search tree data structure. (See Data Structures for Range Searching and Introduction to Algorithms, Second Edition.) The records are stored in the leaves. Each branch of the tree has a discriminator. Records with keys less than the discriminator are stored in the left branch, the other records are stored in the right branch. There are a couple of sensible criteria for determining a discriminator which splits the records. We can split by the median, in which case half the records go to the left branch and half to the right. We recursively split until we have no more than a certain number of records. Let this number be leaf_size. These records, stored in a list or an array, make up a leaf of the tree. The depth of the tree depends only on the number of records.
We can also choose the discriminator to be the midpoint of the interval. If the records span the interval ![$[\alpha .. \beta]$](form_6.png) then all records x that satisfy
then all records x that satisfy 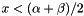 go to the left branch and the other records go to the right. Again, we recursively split until there are no more than leaf_size records at which point we store the records in a leaf. Note that the depth of the tree depends on the distribution of the records.
go to the left branch and the other records go to the right. Again, we recursively split until there are no more than leaf_size records at which point we store the records in a leaf. Note that the depth of the tree depends on the distribution of the records.
Below is the code for constructing a binary search tree. The function returns the root of the tree.
tree_make(records): if records.sizeleaf_size: Make a leaf. leaf.insert(records) return leaf else: Make a branch. Choose the branch.discriminator. left_records = {x
records | x < discriminator} branch.left = tree_make(left_records) right_records = {x
records | x
discriminator} branch.right = tree_make(right_records) return branch
We now consider range queries on records stored in binary search trees. Given a branch and a query range ![$[a .. b]$](form_7.png) , the domain of the left sub-tree overlaps the query range if the discriminator is greater than or equal to a. In this case, the left sub-tree is searched. If the discriminator is less than or equal to b, then the domain of the right sub-tree overlaps the query range and the right sub-tree must be searched. This gives us a prescription for recursively searching the tree. When a leaf is reached, the records are checked with a sequential scan. RQ_tree() performs a range query when called with the root of the binary search tree.
, the domain of the left sub-tree overlaps the query range if the discriminator is greater than or equal to a. In this case, the left sub-tree is searched. If the discriminator is less than or equal to b, then the domain of the right sub-tree overlaps the query range and the right sub-tree must be searched. This gives us a prescription for recursively searching the tree. When a leaf is reached, the records are checked with a sequential scan. RQ_tree() performs a range query when called with the root of the binary search tree.
RQ_tree(node, range = [a..b]):
if node is a leaf:
return RQ_sequential_scan(node.records, range)
else:
included_records = 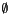 if node.discriminator
if node.discriminator 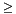 a:
included_records += RQ_tree(node.left, range)
if node.discriminator
a:
included_records += RQ_tree(node.left, range)
if node.discriminator 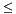 b:
included_records += RQ_tree(node.right, range)
return included_records
b:
included_records += RQ_tree(node.right, range)
return included_records
If the domain of a leaf or branch is a subset of the query range then it is not necessary to check the records for inclusion. We can simply report all of the records in the leaf or sub-tree. (See the tree_report() function below.) This requires that we store the domain at each node (or compute the domain as we traverse the tree). The RQ_tree_domain() function first checks if the domain of the node is a subset of the query range and if not, then checks if the domain overlaps the query range.
tree_report(node):
if node is a leaf:
return node.records
else:
return (tree_report(node.left) + tree_report(node.right))
RQ_tree_domain(node, range = [a..b]): if node.domainrange: return tree_report(node) else: if node is a leaf: return RQ_sequential_scan(node.records, range) else: included_records =
if node.discriminator
a: included_records += RQ_tree(node.left, range) if node.discriminator
b: included_records += RQ_tree(node.right, range) return included_records
RQ_tree() and RQ_tree_domain() have the same computational complexity. The former has better performance when the query range contains few records. The latter performs better when the number of records in the range is larger than leaf_size.
For median splitting, the depth of the tree depends only on the number of records. The computational complexity depends only on the total number of records, N, and the number of records which are reported or checked for inclusion, 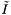 .
.
![\[ \mathrm{Preprocess} = \mathcal{O}(N \log N), \quad \mathrm{Reprocess} = \mathcal{O}(N), \]](form_19.png)
![\[ \mathrm{Storage} = \mathcal{O}(N), \quad \mathrm{Query} = \mathcal{O}(\log N + \tilde{I}) \]](form_25.png)
For midpoint splitting, the depth of the tree D depends on the distribution of records. Thus the computational complexity depends on this parameter. The average case performance of a range query is usually much better than the worst-case computational complexity.
![\[ \mathrm{Preprocess} = \mathcal{O}((D + 1) N), \quad \mathrm{Reprocess} = \mathcal{O}((D + 1) N), \quad \mathrm{Storage} = \mathcal{O}((D + 1) N), \]](form_26.png)
![\[ \mathrm{Query} = \mathcal{O}(N), \quad \mathrm{AverageQuery} = \mathcal{O}(D + \tilde{I}) \]](form_27.png)
Cells or Bucketing
We can apply a bucketing strategy to the range query problem. (See Data Structures for Range Searching.) Consider a uniform partition of the interval ![$[\alpha .. \beta]$](form_6.png) with the points
with the points  .
.
![\[ x_0 = \alpha, \quad x_M > \beta, \quad x_{m+1} - x_m = \frac{x_M - x_0}{M} \]](form_29.png)
The 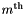 cell (or bucket)
cell (or bucket) 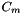 holds the records in the interval
holds the records in the interval 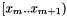 . We have an array of M cells, each of which holds a list or an array of the records in its interval. We can place a record in a cell by converting the key to a cell index. Let the cell array data structure have the attribute min which returns the minimum key in the interval
. We have an array of M cells, each of which holds a list or an array of the records in its interval. We can place a record in a cell by converting the key to a cell index. Let the cell array data structure have the attribute min which returns the minimum key in the interval 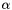 and the attribute delta which returns the size of a cell. The process of putting the records in the cell array is called a cell sort.
and the attribute delta which returns the size of a cell. The process of putting the records in the cell array is called a cell sort.
cell_sort(cells, file):
for record in file:
cells[key_to_cell_index(cells, record.key)] += record
key_to_cell_index(cells, key): return(key - cells.min) / cells.delta
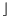
We perform a range query by determining the range of cells ![$[i .. j]$](form_36.png) whose intervals overlap the query range
whose intervals overlap the query range ![$[a .. b]$](form_7.png) . Let J be the number of overlapping cells. The contents of the cells in the range
. Let J be the number of overlapping cells. The contents of the cells in the range ![$[i+1 .. j-1]$](form_37.png) lie entirely in the query range. The contents of the two boundary cells
lie entirely in the query range. The contents of the two boundary cells 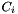 and
and 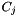 lie partially in the query range. We must check the records in these two cells for inclusion in the query range.
lie partially in the query range. We must check the records in these two cells for inclusion in the query range.
RQ_cell(cells, range = [a .. b]): included_records =i = key_to_cell_index(cells, a) j = key_to_cell_index(cells, b) for x in cells[i]: if x
a: included_records += x for k in [i+1 .. j-1]: for x in cells[k]: included_records += x for x in cells[j]: if x
b: included_records += x return included_records
The preprocessing time is linear in the number of records N and the number of cells M and is accomplished by a cell sort. Reprocessing is done by scanning the contents of each cell and moving records when necessary. Thus reprocessing has linear complexity as well. Since the data structure is an array of cells each containing a list or array of records, the storage requirement is 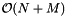 . Let
. Let 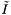 be the number records in the J cells that overlap the query range. The computational complexity of a query is
be the number records in the J cells that overlap the query range. The computational complexity of a query is 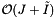 . If the cell size is no larger than the query range, then we expect that
. If the cell size is no larger than the query range, then we expect that 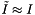 . If the number of records is greater than the number of cells, then the expected computational complexity is
. If the number of records is greater than the number of cells, then the expected computational complexity is 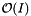 .
.
![\[ \mathrm{Preprocess} = \mathcal{O}(N + M), \quad \mathrm{Reprocess} = \mathcal{O}(N + M), \quad \mathrm{Storage} = \mathcal{O}(N + M), \]](form_44.png)
![\[ \mathrm{Query} = \mathcal{O}(J + \tilde{I}), \quad \mathrm{AverageQuery} = \mathcal{O}(I) \]](form_45.png)
Generated on Thu Jun 30 02:14:58 2016 for Computational Geometry Package by
 1.6.3
1.6.3