Computational Complexity Comparison
The table below gives labels to the orthogonal range query methods that we will compare. It also gives a reference to the section in which the method is introduced. Related methods are grouped together.
| label | description | reference |
|---|---|---|
| seq. scan | sequential scan | section |
| projection | projection | section |
| pt-in-box | point-in-box | section |
| kd-tree | kd-tree | section |
| kd-tree d. | kd-tree with domain checking | section |
| octree | octree | section |
| cell | cell array | section |
| sparse cell | sparse cell array | section |
| cell b. s. | cell array with binary search | section |
| cell f. s. | cell array with forward search | section |
| cell f. s. k. | cell array with forward search on keys | section |
Labels and references for the orthogonal range query methods.
The table below lists the expected computational complexity for an orthogonal range query and the storage requirements of the data structure for each of the presented methods. We consider the case that the query range is small and cubical. To review the notation: There are N records in K-dimensional space. There are I records in the query range. There are M cells in the dense cell array method. R is the ratio of the length of a query range to the length of a cell in a given coordinate. The depth of the octree is D. For multiple query methods, Q is the number of queries.
| Method | Expected Complexity of ORQ | Storage |
|---|---|---|
| seq. scan | N | N |
| projection | 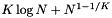 | K N |
| pt-in-box | 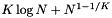 | 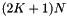 |
| kd-tree | 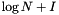 | N |
| kd-tree d. | 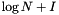 | N |
| octree | 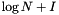 | 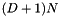 |
| cell | 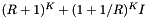 | M + N |
| sparse cell | 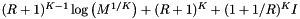 | 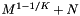 |
| cell b. s. | 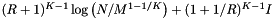 | 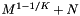 |
| cell f. s. | 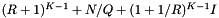 | 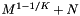 |
| cell f. s. k. | 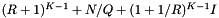 | 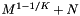 |
Computational complexity and storage requirements for the orthogonal range query methods.
The sequential scan is the brute force method and is rarely practical.
For the projection and point-in-box methods the 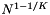 term, which is the expected number of records in a slice, typically dominates the query time. This strong dependence on N means that the projection methods are usually suitable when the number of records is small. The projection methods also have a fairly high storage overhead, storing either K or
term, which is the expected number of records in a slice, typically dominates the query time. This strong dependence on N means that the projection methods are usually suitable when the number of records is small. The projection methods also have a fairly high storage overhead, storing either K or 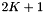 arrays of length N.
arrays of length N.
Although the leaf size does not appear in the computational complexity or storage complexity, choosing a good leaf size is fairly important in getting good performance from tree methods.
Dense cell array methods are attractive when the distribution of records is such that the memory overhead of the cells is not too high. A uniform distribution of records would be the best case. If one can afford the memory overhead of cells, then one can often choose a cell size that balances the cost of cell accesses, 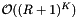 , and inclusion tests,
, and inclusion tests, 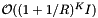 , to obtain a method that is close to linear complexity in the number of included records.
, to obtain a method that is close to linear complexity in the number of included records.
If the dense cell array method requires too much memory, then a sparse cell array or a cell array coupled with a binary search on records may give good performance. Both use a binary search; the former to access cells and the latter to access records. Often the cost of the binary searches, (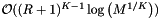 and
and 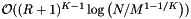 , respectively), is small compared to the costs of the inclusion tests. This is because the number of cells,
, respectively), is small compared to the costs of the inclusion tests. This is because the number of cells, 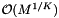 , or the number of records,
, or the number of records, 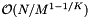 , in the search is small.
, in the search is small.
For multiple query problems, if the total number T of records in query ranges is at least as large as the number of records N then a cell array coupled with forward searching will likely give good performance. In this case the cost of the searching, 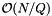 , will be small and the cell size can be chosen to balance the cost of accessing cells,
, will be small and the cell size can be chosen to balance the cost of accessing cells, 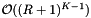 , with the cost of inclusion tests,
, with the cost of inclusion tests, 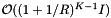 .
.
Generated on Thu Jun 30 02:14:58 2016 for Computational Geometry Package by
 1.6.3
1.6.3