Multiple Orthogonal Range Queries

Cells Coupled with Forward Searching

In this section we extend the algorithm for doing multiple 1-D range queries to higher dimensions. Note that one can couple the cell method with other search data structures. For instance, one could sort the records in each of the cells or store those records in a search tree. Most such combinations of data structures do not offer any advantages. However, there are some that do. For example, we coupled a binary search to a cell array. For this data structure, we can access a record with array indexing in the first K - 1 dimensions and a binary search in the final dimension.

Coupling the forward search of the previous section, which was designed for multiple queries, with a cell array makes sense. The data structure is little changed. Again there is a dense cell array which spans K - 1 dimensions. In each cell, we store records sorted in the remaining dimension. However, now each cell has the first_in_range attribute. In performing range queries, we access records with array indexing in K - 1 dimensions and a forward search in the final dimension.

We construct the data structure by cell sorting the records and then sorting the records within each cell. Then we sort the query ranges by their minimum key in the final dimension. Let the data structure have the attribute min which returns the minimum multikey in the domain and the attribute delta which returns the size of a cell. Let cells be the cell array. Below are the functions for constructing and initializing the data structure.

construct(file):
  for record in file:
    cells[multikey_to_cell_index(record.multikey)] += record
  for cell in cells:
    sort_by_last_key(cell)
  sort_by_last_key(queries)
  return

multikey_to_cell_index(multikey):
  for k  [0..K-1):
    index[k] (multikey[k] - min[k]) / delta[k]
  return index

initialize():
  for cell in cells:
    cell.first_in_range = cell.begin

Each orthogonal range query consists of accessing cells that overlap the domain and then doing a forward search followed by a sequential scan on the sorted records in each of these cells. Below is the orthogonal range query method.

MORQ_cell_forward_search(range):
  included_records = 
  min_index = multikey_to_index(range.min)
  max_index = multikey_to_index(range.max)
  for index in [min_index..max_index]:
    cell = cells[index]
    while (cell.first_in_range  cell.end and (*cell.first_in_range).multikey[K-1] < range.min[K-1]):
      ++cell.first_in_range
    iter = cell.first_in_range
    while (*iter).multikey[K-1]  range.max[K-1]:
      if *iter  range:
        included_records += iter
      ++iter
  return included_records

As with cell arrays with binary searching, the query performance depends on the size of the cells and the query range. The same results carry over. The only difference is that the binary search on records is replaced with a forward search. If the total number of records in ranges, T, is at least as large as the number of records N, then we expect the forward searching to be less costly. The preprocessing time for the cell array with binary search is 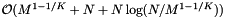$\mathcal{O}( M^{1 - 1/K} + N + N \log(N / M^{1- 1/K}) )$ . For the forward search method we must also sort the Q queries, so the preprocessing complexity is 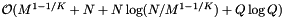$\mathcal{O}( M^{1 - 1/K} + N + N \log(N / M^{1- 1/K}) + Q \log Q )$ . The reprocessing time for the cell array with binary search is 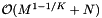$\mathcal{O}(M^{1 - 1/K} + N)$ . If the records and query ranges change by small amounts, we can use insertion sort (combined with cell sort for the records) to resort them. Thus the reprocessing complexity for the forward search method is 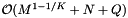$\mathcal{O}(M^{1 - 1/K} + N + Q)$ . The forward search method requires that we store the sorted query ranges. 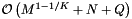This the storage requirement is $\mathcal{O} \left( M^{1 - 1/K} + N + Q \right)$ .

We will determine the expected cost of a query. Let I the number of records in a single query range. Let J be the number of cells which overlap the query range and 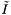$\tilde{I}$ be the number of records which are reported or checked for inclusion in the overlapping cells. There will be J forward searches to find the starting record in each cell. The total cost of the forward searches for all the queries (excluding the cost of starting the search in each cell) is 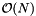$\mathcal{O}(N)$ . Thus the average cost of the forward searching per query is 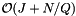$\mathcal{O}(J + N/Q)$ . As with the binary search method, we suppose that the cells are no larger than the query range and that both are roughly cubical (except in the forward search direction). Let R be the ratio of the length of a query range to the length of a cell in a given coordinate. In this case 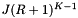$J \lesssim (R + 1)^{K-1}$ . The number of records in the overlapping cells that are checked for inclusion is about 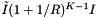$\tilde{I} \lesssim (1 + 1/R)^{K-1} I$ . The inclusion tests add a cost of 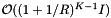$\mathcal{O}((1 + 1/R)^{K-1} I)$ . 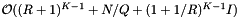Thus the average cost of a single query is $\mathcal{O}( (R + 1)^{K-1} + N/Q + (1 + 1/R)^{K-1} I )$ .

$\mathrm{Preprocess} = \mathcal{O} \left( M^{1 - 1/K} + N + N \log(N / M^{1- 1/K}) + Q \log Q \right),$

$\mathrm{Reprocess} = \mathcal{O} \left( M^{1 - 1/K} + N + Q \right), \quad \mathrm{Storage} = \mathcal{O} \left( M^{1 - 1/K} + N + Q \right),$

$\mathrm{AverageQuery} = \mathcal{O} \left( (R + 1)^{K-1} + N/Q + (1 + 1/R)^{K-1} I \right),$

$\mathrm{TotalQueries} = \mathcal{O} \left( Q (R + 1)^{K-1} + N + (1 + 1/R)^{K-1} T \right),$

The figures below show the execution times and storage requirements for the chair problem. The performance is similar to the cell array coupled with binary searching. As expected, the execution times are lower, and the memory usage is higher. Because the forward searching is less costly than the binary searching, the forward search method is less sensitive to cell size. It has a larger "sweet spot." For this test, the best execution times are obtained when R is between 1/8 and 1/2.

The effect of leaf size on the performance of the cell array coupled with forward searches for the chair problem. The plot shows the execution time in seconds versus R. The performance of the cell array coupled with binary searches is shown for comparison.

The effect of leaf size on the performance of the cell array coupled with forward searches for the chair problem. The plot shows the memory usage in megabytes versus R. The performance of the cell array coupled with binary searches is shown for comparison.

The figures below show the execution times and storage requirements for the random points problem. The execution times are better than those for the cell array with binary searching. This improvement is significant near the sweet spot, but diminishes when the cell size is not tuned to the query size. There is an increase in memory usage from the binary search method.

The effect of leaf size on the performance of the cell array coupled with forward searches for the random points problem. The plot shows the execution time in seconds versus R. The performance of the cell array coupled with binary searches is shown for comparison.

The effect of leaf size on the performance of the cell array coupled with forward searches for the random points problem. The plot shows the memory usage in megabytes versus R. The performance of the cell array coupled with binary searches is shown for comparison.

In the figures below we show the best cell size versus the query range size for the random points problem. As with the cell array with binary searching, we see that the best cell size for this problem is not correlated to the query size.

The best cell size versus the query range size for the cell array coupled with forward searches on the random points problem.

The ratio of the cell size to the query range size.

Storing the Keys

The most expensive part of doing the orthogonal range queries with the cell array coupled with forward searching is actually just accessing the records and their keys. This is because the search method is very efficient and the forward search needs to access the records. To cut the cost of accessing the records and their keys, we can store the keys in the data structure. This will reduce the cost of the forward searches and the inclusion tests. However, there will be a substantial increase in memory usage. We will examine the effect of storing the keys.

The figures below show the execution times and storage requirements for the chair problem. The performance has the same characteristics as the data structure that does not store the keys. By storing the keys, we roughly cut the execution time in half. However, there is a fairly large storage overhead. Instead of just storing a pointer to the record, we store the pointer and three keys. In this example, the keys are double precision numbers. Thus the memory usage goes up by about a factor of seven. If the keys had been integers or single precision floats, the increase would have been smaller.

The effect of leaf size on the performance of the cell array that stores keys and uses forward searches for the chair problem. The plot shows the execution time in seconds versus R. The performance of the data structure that does not store the keys is shown for comparison.

The effect of leaf size on the performance of the cell array that stores keys and uses forward searches for the chair problem. The plot shows the memory usage in megabytes versus R. The performance of the data structure that does not store the keys is shown for comparison.

The figures below show the execution times and storage requirements for the random points problem. Again we see that storing the keys improves the execution time at the price of increased memory usage.

The effect of leaf size on the performance of the cell array coupled with forward searches that stores the keys for the random points problem. The plot shows the execution time in seconds versus R. The performance of the data structure that does not store the keys is shown for comparison.

The effect of leaf size on the performance of the cell array coupled with forward searches that stores the keys for the random points problem. The plot shows the memory usage in megabytes versus R. The performance of the data structure that does not store the keys is shown for comparison.

Generated on Thu Jun 30 02:14:58 2016 for Computational Geometry Package by 1.6.3