SimplexMeanRatio< N, T > Class Template Reference
Implements the mean ratio quality metric. More...
#include <SimplexMeanRatio.h>

Public Types | |
| typedef T | Number |
| The number type. | |
| typedef Base::Vertex | Vertex |
| The class for a vertex. | |
| typedef Base::Simplex | Simplex |
| The simplex type. | |
| typedef Base::Matrix | Matrix |
| An NxN matrix. | |
Public Member Functions | |
Constructors etc. | |
| SimplexMeanRatio () | |
| Default constructor. Un-initialized memory. | |
| SimplexMeanRatio (const SimplexMeanRatio &other) | |
| Copy constructor. | |
| SimplexMeanRatio (const Simplex &s) | |
| Construct from a simplex. | |
| SimplexMeanRatio & | operator= (const SimplexMeanRatio &other) |
| Assignment operator. | |
| ~SimplexMeanRatio () | |
| Trivial destructor. | |
Mathematical functions | |
| Number | operator() () const |
| Return the mean ratio (eta) quality metric. | |
| Number | operator() (const Simplex &simplex) const |
| Return the mean ratio (eta) quality metric. | |
| void | computeGradient (Vertex *gradient) const |
| Calculate the gradient of the mean ratio (eta) quality metric. | |
Protected Member Functions | |
| Number | computeFunctionGivenS2 (Number s2) const |
Return the eta quality metric given 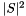 . . | |
Detailed Description
template<int N, typename T = double>
class SimplexMeanRatio< N, T >
Implements the mean ratio quality metric.
- Parameters:
-
N is the dimension. T is the number type. By default it is double.
This class implements the mean ratio quality metric. Let 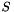 be the Jacobian matrix,
be the Jacobian matrix, 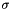 be the Jacobian determinant and
be the Jacobian determinant and 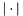 be the Frobenius norm. The
be the Frobenius norm. The operator() member function returns the mean ratio quality metric:
![\[ \eta = \frac{ |S|^2 }{ N \sigma^{2/N} }. \]](form_216.png)
This quality metric is only defined for simplices with positive content. (The Jacobian determinant must be positive.)
computeGradient() calculates the gradient of the mean ratio metric.
Before evaluating the mean ratio metric, you must set the Jacobian matrix with setFunction() or set(). Before evaluating the gradient of the metric, you must set the Jacobian matrix and its gradient with set().
Member Function Documentation
| void SimplexMeanRatio< N, T >::computeGradient | ( | Vertex * | gradient | ) | const |
Calculate the gradient of the mean ratio (eta) quality metric.
- Precondition:
- The Jacobian determinant must be positive.
Let 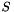 be the Jacobian matrix,
be the Jacobian matrix, 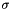 be the Jacobian determinant and
be the Jacobian determinant and 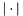 be the Frobenius norm. The eta function is
be the Frobenius norm. The eta function is
![\[ \frac{ |S|^2 }{ N \sigma^{2/N} }. \]](form_217.png)
Reimplemented in SimplexModMeanRatio< N, T >.
| Number SimplexMeanRatio< N, T >::operator() | ( | const Simplex & | simplex | ) | const [inline] |
Return the mean ratio (eta) quality metric.
- Precondition:
- The Jacobian determinant must be positive.
- Returns:
- Let
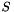 be the Jacobian matrix,
be the Jacobian matrix, 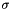 be the Jacobian determinant and
be the Jacobian determinant and 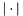 be the Frobenius norm. Return
be the Frobenius norm. Return ![\[ \frac{ |S|^2 }{ N \sigma^{2/N} }. \]](form_217.png)
Reimplemented in SimplexModMeanRatio< N, T >.
References SimplexMeanRatio< N, T >::operator()(), and SimplexJacQF< N, T >::setFunction().
| Number SimplexMeanRatio< N, T >::operator() | ( | ) | const |
Return the mean ratio (eta) quality metric.
- Precondition:
- The Jacobian determinant must be positive.
- Returns:
- Let
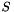 be the Jacobian matrix,
be the Jacobian matrix, 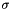 be the Jacobian determinant and
be the Jacobian determinant and 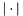 be the Frobenius norm. Return
be the Frobenius norm. Return ![\[ \frac{ |S|^2 }{ N \sigma^{2/N} }. \]](form_217.png)
Reimplemented in SimplexModMeanRatio< N, T >.
Referenced by SimplexMeanRatio< N, T >::operator()().
The documentation for this class was generated from the following file:
Generated on Thu Jun 30 02:14:58 2016 for Computational Geometry Package by
 1.6.3
1.6.3