Simplex< N, V, T > Class Template Reference

A simplex in N dimensions. More...

#include <Simplex.h>

Public Types
typedef V	Vertex
	The vertex type.
typedef T	Number
	The number type.
typedef ads::FixedArray< N+1, Vertex >	VertexContainer
	The container for the vertices.
typedef VertexContainer::value_type	Value
	The vertex type.
typedef VertexContainer::iterator	Iterator
	An iterator on the vertices.
typedef VertexContainer::const_iterator	ConstIterator
	A const iterator on the vertices.
typedef VertexContainer::reference	Reference
	A reference to a vertex.
typedef VertexContainer::const_reference	ConstReference
	A const reference to a vertex.
typedef VertexContainer::parameter_type	Parameter
	A parameter type for a vertex.
typedef Simplex< N-1, V, T >	Face
	The (N-1)-face of an N-simplex.
Public Member Functions
Constructors etc.

	Simplex ()
	Default constructor. Un-initialized memory.
	Simplex (const Simplex &other)
	Copy constructor.
	Simplex (const VertexContainer &vertices)
	Construct from the vertices.
void	build (const VertexContainer &vertices)
	Build from the vertices.
	Simplex (Parameter v)
	Construct a 0-D simplex from a vertex.
void	build (Parameter v)
	Build a 0-D simplex from a vertex.
	Simplex (Parameter v0, Parameter v1)
	Construct a 1-D simplex from two vertices.
void	build (Parameter v0, Parameter v1)
	Build a 1-D simplex from two vertices.
	Simplex (Parameter v0, Parameter v1, Parameter v2)
	Construct a 2-D simplex from three vertices.
void	build (Parameter v0, Parameter v1, Parameter v2)
	Build a 2-D simplex from three vertices.
	Simplex (Parameter v0, Parameter v1, Parameter v2, Parameter v3)
	Construct a 3-D simplex from four vertices.
void	build (Parameter v0, Parameter v1, Parameter v2, Parameter v3)
	Build a 3-D simplex from four vertices.
template<typename VertRAIter , typename IndSimp >
	Simplex (VertRAIter vertices, const IndSimp &indexed_simplex)
	Construct from an array of vertices and and indexed simplex.
template<typename VertRAIter , typename IndSimp >
void	build (VertRAIter vertices, const IndSimp &indexed_simplex)
	Build from an array of vertices and and indexed simplex.
Simplex &	operator= (const Simplex &other)
	Assignment operator.
	~Simplex ()
	Trivial destructor.
STL-style Accessors.

ConstIterator	begin () const
	Return a const iterator to the beginning of the vertices.
ConstIterator	end () const
	Return a const iterator to the end of the vertices.
int	size () const
	Return the number of vertices.
Accessors

const VertexContainer &	getVertices () const
	Return a const reference to the vertex container.
Parameter	operator[] (const int n) const
	Return the n_th vertex.
ConstIterator	getBeginning () const
	Return a const iterator to the beginning of the vertices.
ConstIterator	getEnd () const
	Return a const iterator to the end of the vertices.
int	getSize () const
	Return the number of vertices.
template<typename Comparable >
bool	hasVertex (const Comparable &v) const
	Return true if the simplex has the given vertex.
template<typename Comparable >
bool	hasVertex (const Comparable &v, int *n) const
	Return true if the simplex has the given vertex.
template<int M>
bool	hasFace (const Simplex< M, V, T > &f) const
	Return true if the simplex has the given face as a sub-simplex.
template<typename Comparable >
int	getVertexIndex (const Comparable &v) const
	Return the index of the given vertex.
Face	getFace (const int n) const
	Return the face obtained by removing the n_th vertex.
void	getFace (const int n, Face *f) const
	Get the face obtained by removing the n_th vertex.
void	computeBBox (BBox< N, Number > *bb) const
	Calculate a bounding box around the simplex.
void	computeCentroid (Vertex *centroid) const
	Calculate the centroid of the simplex.
STL-style Manipulators.

Iterator	begin ()
	Return an iterator to the beginning of the vertices.
Iterator	end ()
	Return an iterator to the end of the vertices.
Manipulators

Reference	operator[] (const int n)
	Return a reference to the n_th vertex.
Iterator	getBeginning ()
	Return an iterator to the beginning of the vertices.
Iterator	getEnd ()
	Return an iterator to the end of the vertices.
void	set (const VertexContainer &vertices)
	Set the vertices.
void	setEach (Parameter value)
	Set each vertex to the specified value.
void	negate ()
	Reverse the orientation of the simplex.
Related Functions
(Note that these are not member functions.)
template<typename T >
BEGIN_NAMESPACE_GEOM T	computeAngle (const Simplex< 3, ads::FixedArray< 3, T >, T > &s, int a, int b)
	The dihedral angle between two faces.
template<typename T >
T	computeAngle (const Simplex< 3, ads::FixedArray< 3, T >, T > &s, int n)
	The solid angle at a vertex.
template<typename T >
void	projectToLowerDimension (const Simplex< 1, ads::FixedArray< 2, T >, T > &s, Simplex< 1, ads::FixedArray< 1, T >, T > *t)
	Project the simplex to a lower dimension.
template<typename T >
void	projectToLowerDimension (const Simplex< 1, ads::FixedArray< 3, T >, T > &s, Simplex< 1, ads::FixedArray< 1, T >, T > *t)
	Project the simplex to a lower dimension.
template<typename T >
void	projectToLowerDimension (const Simplex< 2, ads::FixedArray< 3, T >, T > &s, Simplex< 2, ads::FixedArray< 2, T >, T > *t)
	Project the simplex to a lower dimension.
template<int N, typename V , typename T >
bool	operator== (const Simplex< N, V, T > &x, const Simplex< N, V, T > &y)
	Return true if the vertices are given in the same order.
template<int N, typename V , typename T >
bool	operator!= (const Simplex< N, V, T > &x, const Simplex< N, V, T > &y)
	Return true if the vertices are not given in the same order.
template<typename V , typename T >
bool	haveSameOrientation (const Simplex< 0, V, T > &x, const Simplex< 0, V, T > &y)
	Return true if the two simplices have the same orientation.
template<typename V , typename T >
bool	haveSameOrientation (const Simplex< 1, V, T > &x, const Simplex< 1, V, T > &y)
	Return true if the two simplices have the same orientation.
template<typename V , typename T >
bool	haveSameOrientation (const Simplex< 2, V, T > &x, const Simplex< 2, V, T > &y)
	Return true if the two simplices have the same orientation.
template<int N, typename V , typename T >
std::ostream &	operator<< (std::ostream &out, const Simplex< N, V, T > &x)
	Write the vertices.
template<int N, typename V , typename T >
std::istream &	operator>> (std::istream &in, Simplex< N, V, T > &x)
	Read the vertices.
template<typename T >
BEGIN_NAMESPACE_GEOM bool	isIn (const Simplex< 1, ads::FixedArray< 1, T >, T > &s, const ads::FixedArray< 1, T > &x)
	Return true if the 1-D point is inside the 1-D simplex.
template<typename T >
bool	isIn (const Simplex< 2, ads::FixedArray< 2, T >, T > &s, const ads::FixedArray< 2, T > &x)
	Return true if the 2-D point is inside the 2-D simplex.
template<typename T >
bool	isIn (const Simplex< 3, ads::FixedArray< 3, T >, T > &s, const ads::FixedArray< 3, T > &x)
	Return true if the 3-D point is inside the 3-D simplex.
template<typename T >
T	computeDistanceInterior (const Simplex< 1, ads::FixedArray< 1, T >, T > &s, const ads::FixedArray< 1, T > &x)
	Compute the distance from the 1-D, interior point to the 1-D simplex.
template<typename T >
T	computeDistanceInterior (const Simplex< 2, ads::FixedArray< 2, T >, T > &s, const ads::FixedArray< 2, T > &x)
	Compute the distance from the 2-D, interior point to the 2-D simplex.
template<typename T >
T	computeDistanceInterior (const Simplex< 3, ads::FixedArray< 3, T >, T > &s, const ads::FixedArray< 3, T > &x)
	Compute the distance from the 3-D, interior point to the 3-D simplex.
template<typename T >
T	computeDistance (const Simplex< 1, ads::FixedArray< 1, T >, T > &s, const ads::FixedArray< 1, T > &x)
	Compute the signed distance from the 1-D point to the 1-D simplex.
template<typename T >
T	computeDistance (const Simplex< 1, ads::FixedArray< 2, T >, T > &s, const ads::FixedArray< 2, T > &x)
	Compute the unsigned distance from the 2-D point to the 1-D simplex.
template<typename T >
T	computeDistance (const Simplex< 1, ads::FixedArray< 3, T >, T > &s, const ads::FixedArray< 3, T > &x)
	Compute the unsigned distance from the 3-D point to the 1-simplex.
template<typename T >
T	computeDistance (const Simplex< 2, ads::FixedArray< 2, T >, T > &s, const ads::FixedArray< 2, T > &x)
	Compute the signed distance from the 2-D point to the 2-D simplex.
template<typename T >
T	computeDistance (const Simplex< 2, ads::FixedArray< 3, T >, T > &s, const ads::FixedArray< 3, T > &x)
	Compute the unsigned distance from the 3-D point to the 2-D simplex.
template<typename T >
T	computeDistance (const Simplex< 3, ads::FixedArray< 3, T >, T > &s, const ads::FixedArray< 3, T > &x)
	Compute the signed distance from the 3-D point to the 3-D simplex.
template<typename T >
T	computeUnsignedDistance (const Simplex< 1, ads::FixedArray< 1, T >, T > &s, const ads::FixedArray< 1, T > &x)
	Compute the unsigned distance from the 1-D point to the 1-D simplex.
template<typename T >
T	computeUnsignedDistance (const Simplex< 2, ads::FixedArray< 2, T >, T > &s, const ads::FixedArray< 2, T > &x)
	Compute the unsigned distance from the 2-D point to the 2-D simplex.
template<typename T >
T	computeUnsignedDistance (const Simplex< 3, ads::FixedArray< 3, T >, T > &s, const ads::FixedArray< 3, T > &x)
	Compute the unsigned distance from the 3-D point to the 3-D simplex.
template<int N, typename T >
T	computeSignedDistance (const ads::FixedArray< N, T > &p, const ads::FixedArray< N, T > &n, const ads::FixedArray< N, T > &x)
	Compute the signed distance from the N-D point with normal to the N-D point.
template<typename T >
T	computeSignedDistance (const Simplex< 1, ads::FixedArray< 2, T >, T > &s, const ads::FixedArray< 2, T > &x)
	Compute the signed distance from the 2-D point to the 1-simplex.
template<typename T >
T	computeSignedDistance (const Simplex< 1, ads::FixedArray< 2, T >, T > &s, const ads::FixedArray< 2, T > &x, ads::FixedArray< 2, T > *closestPoint)
	Compute the signed distance and closest point from the 2-D point to the 1-simplex.
template<typename T >
T	computeSignedDistance (const Simplex< 2, ads::FixedArray< 3, T >, T > &s, const ads::FixedArray< 3, T > &x)
	Compute the signed distance from the 3-D point to the 2-simplex.
template<typename T >
T	computeSignedDistance (const Simplex< 2, ads::FixedArray< 3, T >, T > &s, const ads::FixedArray< 3, T > &n, const ads::FixedArray< 3, T > &x, ads::FixedArray< 3, T > *closestPoint)
	Compute the signed distance and closest point from the 3-D point to the 2-simplex.
template<typename T >
T	computeSignedDistance (const Simplex< 1, ads::FixedArray< 3, T >, T > &s, const ads::FixedArray< 3, T > &n, const ads::FixedArray< 3, T > &x)
	Compute the signed distance from the 3-D point to the 1-simplex with normal.
template<typename T >
T	computeSignedDistance (const Simplex< 1, ads::FixedArray< 3, T >, T > &s, const ads::FixedArray< 3, T > &n, const ads::FixedArray< 3, T > &x, ads::FixedArray< 3, T > *closestPoint)
	Compute the signed distance and closest point from the 3-D point to the 1-simplex with normal.
template<typename T >
T	computeClosestPoint (const Simplex< 1, ads::FixedArray< 2, T >, T > &simplex, const ads::FixedArray< 2, T > &point, ads::FixedArray< 2, T > *closestPoint)
	Return the unsigned distance from the 2-D point to the 1-D simplex and compute the closest point.
BEGIN_NAMESPACE_GEOM void	computeOtherIndices (int i, int j, int a, int b)
	Compute the other indices of the simplex.
int	computeOtherIndex (int i, int j, int k)
	Compute the other index of the simplex.
template<int N, typename V , typename T >
bool	hasFace (const Simplex< N, V, T > &simplex, const typename Simplex< N, V, T >::Face &face, int *faceIndex)
	Return true if the N-simplex has the specified (N-1)-face.
template<int N, typename V , typename T >
bool	hasFace (const Simplex< N, V, T > &simplex, const typename Simplex< N, V, T >::Face &face)
	Return true if the N-simplex has the specified (N-1)-face.
template<typename V , typename T >
bool	hasFace (const Simplex< 3, V, T > &simplex, const V &x, const V &y, const V &z)
	Return true if the 3-simplex has the face specified by the three vertices.
template<typename V , typename T >
bool	hasFace (const Simplex< 3, V, T > &simplex, const V &x, const V &y, const V &z, int *faceIndex)
	Return true if the 3-simplex has the face specified by the three vertices.

Detailed Description

template<int N, typename V, typename T = double>
class Simplex< N, V, T >

A simplex in N dimensions.

Parameters:

	N	is the dimension.
	V	is the vertex type.
	T	is the number type. By default it is double.

This simplex stores N+1 vertices. It does not store them in lexicographical order. This has the advantage that we do not need to store a sign. Then we can treat a container of N+1 vertices as a simplex. It has the disadvantage that it is difficult to compare simplices for equivalence. (Simplices are equivalent if the vertices of one are an even permutation of the vertices of the other.)

Usage

One can represent a N-simplex in with Cartesian points as vertices by choosing ads::FixedArray<N,double> for the vertex type.

  geom::Simplex< N, ads::FixedArray<N,double> > simplex;

One can represent an indexed simplex for use in an indexed simplex set (see geom::IndexedSimplexSet) by choosing an int for the vertex type.

  geom::Simplex<N,int> indexedSimplex;

Member Function Documentation

template<int N, typename V, typename T = double>

void Simplex< N, V, T >::getFace	(	const int	n,
		Face *	f
	)			const

Get the face obtained by removing the n_th vertex.

For the simplex (v[0], ... v[N]) the face is (-1)^n (v[0], ..., v[n-1], v[n+1], ..., v[N]).

template<int N, typename V, typename T = double>

Face Simplex< N, V, T >::getFace ( const int n ) const [inline]

Return the face obtained by removing the n_th vertex.

For the simplex (v[0], ... v[N]) return (-1)^n (v[0], ..., v[n-1], v[n+1], ..., v[N]).

Referenced by SmrCell< SMR >::getFace(), and Simplex< M, NodeIterator >::getFace().

template<int N, typename V, typename T = double>

template<int M>

bool Simplex< N, V, T >::hasFace ( const Simplex< M, V, T > & f ) const [inline]

Return true if the simplex has the given face as a sub-simplex.

This function does not check the orientation of the face. It returns true if the simplex has each of the vertices in the face.

template<int N, typename V, typename T = double>

template<typename Comparable >

bool Simplex< N, V, T >::hasVertex	(	const Comparable &	v,
		int *	n
	)			const `[inline]`

Return true if the simplex has the given vertex.

If true, compute the index of the vertex.

Friends And Related Function Documentation

template<typename T >

T computeClosestPoint	(	const Simplex< 1, ads::FixedArray< 2, T >, T > &	simplex,
		const ads::FixedArray< 2, T > &	point,
		ads::FixedArray< 2, T > *	closestPoint
	)			`[related]`

Return the unsigned distance from the 2-D point to the 1-D simplex and compute the closest point.

Parameters:

	simplex	is a 1-D simplex (a line segment) in 2-D space.
	point	is a Cartesian point in 2-D space.
	closestPoint	is the closest point on the simplex.

Returns:: the unsigned distance from the point to the simplex.

template<typename T >

T computeDistance	(	const Simplex< 3, ads::FixedArray< 3, T >, T > &	s,
		const ads::FixedArray< 3, T > &	x
	)			`[related]`

Compute the signed distance from the 3-D point to the 3-D simplex.

Parameters:

	s	is a 3-D simplex (a tetrahedron) in 3-D space with Cartesian points as vertices.
	x	is a Cartesian point.

Returns:: the signed distance from the point to the simplex.

template<typename T >

T computeDistance	(	const Simplex< 2, ads::FixedArray< 3, T >, T > &	s,
		const ads::FixedArray< 3, T > &	x
	)			`[related]`

Compute the unsigned distance from the 3-D point to the 2-D simplex.

Parameters:

	s	is a 2-simplex (a triangle) in 3-D space with 3-D Cartesian points as vertices.
	x	is a 3-D Cartesian point.

Returns:: the unsigned distance from the point to the simplex.

template<typename T >

T computeDistance	(	const Simplex< 2, ads::FixedArray< 2, T >, T > &	s,
		const ads::FixedArray< 2, T > &	x
	)			`[related]`

Compute the signed distance from the 2-D point to the 2-D simplex.

Parameters:

	s	is a 2-D simplex (a triangle) in 2-D space with Cartesian points as vertices.
	x	is a Cartesian point.

Returns:: the signed distance from the point to the simplex.

template<typename T >

T computeDistance	(	const Simplex< 1, ads::FixedArray< 3, T >, T > &	s,
		const ads::FixedArray< 3, T > &	x
	)			`[related]`

Compute the unsigned distance from the 3-D point to the 1-simplex.

Parameters:

	s	is a 1-simplex (a line segment) in 3-D space.
	x	is a Cartesian point in 3-D space.

Returns:: the unsigned distance from the point to the simplex.

template<typename T >

T computeDistance	(	const Simplex< 1, ads::FixedArray< 2, T >, T > &	s,
		const ads::FixedArray< 2, T > &	x
	)			`[related]`

Compute the unsigned distance from the 2-D point to the 1-D simplex.

Parameters:

	s	is a 1-D simplex (a line segment) in 2-D space.
	x	is a Cartesian point in 2-D space.

Returns:: the unsigned distance from the point to the simplex.

template<typename T >

T computeDistance	(	const Simplex< 1, ads::FixedArray< 1, T >, T > &	s,
		const ads::FixedArray< 1, T > &	x
	)			`[related]`

Compute the signed distance from the 1-D point to the 1-D simplex.

Parameters:

	s	is a 1-D simplex (an interval) in 1-D space.
	x	is a Cartesian point.

Returns:: the signed distance from the point to the simplex.

template<typename T >

T computeDistanceInterior	(	const Simplex< 3, ads::FixedArray< 3, T >, T > &	s,
		const ads::FixedArray< 3, T > &	x
	)			`[related]`

Compute the distance from the 3-D, interior point to the 3-D simplex.

Parameters:

	s	is a 3-D simplex (a tetrahedron) in 3-D space with Cartesian points as vertices.
	x	is a point that lies inside the simplex.

The point must be inside the simplex. This means that the distance will be non-positive.

Returns:: the distance from the point to the simplex.

template<typename T >

T computeDistanceInterior	(	const Simplex< 2, ads::FixedArray< 2, T >, T > &	s,
		const ads::FixedArray< 2, T > &	x
	)			`[related]`

Compute the distance from the 2-D, interior point to the 2-D simplex.

Parameters:

	s	is a 2-D simplex (a triangle) in 2-D space with Cartesian points as vertices.
	x	is a point that lies inside the simplex.

The point must be inside the simplex. This means that the distance will be non-positive.

Returns:: the distance from the point to the simplex.

template<typename T >

T computeDistanceInterior	(	const Simplex< 1, ads::FixedArray< 1, T >, T > &	s,
		const ads::FixedArray< 1, T > &	x
	)			`[related]`

Compute the distance from the 1-D, interior point to the 1-D simplex.

Parameters:

	s	is a 1-D simplex (an interval) in 1-D space.
	x	is a point that lies inside the simplex.

The point must be inside the simplex. This means that the distance will be non-positive.

Returns:: the distance from the point to the simplex.

template<typename T >

T computeSignedDistance	(	const Simplex< 1, ads::FixedArray< 3, T >, T > &	s,
		const ads::FixedArray< 3, T > &	n,
		const ads::FixedArray< 3, T > &	x,
		ads::FixedArray< 3, T > *	closestPoint
	)			`[related]`

Compute the signed distance and closest point from the 3-D point to the 1-simplex with normal.

Parameters:

	s	is a 1-simplex (a line segment) in 3-D space.
	n	is a normal direction for line segment. The normal direction determines the sign of the distance.
	x	is a Cartesian point in 3-D space.
	closestPoint	is the closest point on the simplex.

Returns:: the signed distance from the point to the simplex. The signed distance is defined above and below the line segment, but not to the side. If the point is not above or below the simplex, return std::numeric_limits<T>::max().

template<typename T >

T computeSignedDistance	(	const Simplex< 1, ads::FixedArray< 3, T >, T > &	s,
		const ads::FixedArray< 3, T > &	n,
		const ads::FixedArray< 3, T > &	x
	)			`[related]`

Compute the signed distance from the 3-D point to the 1-simplex with normal.

Parameters:

	s	is a 1-simplex (a line segment) in 3-D space.
	n	is a normal direction for line segment. The normal direction determines the sign of the distance.
	x	is a Cartesian point in 3-D space.

Returns:: the signed distance from the point to the simplex. The signed distance is defined above and below the line segment, but not to the side. If the point is not above or below the simplex, return std::numeric_limits<T>::max().

template<typename T >

T computeSignedDistance	(	const Simplex< 2, ads::FixedArray< 3, T >, T > &	s,
		const ads::FixedArray< 3, T > &	n,
		const ads::FixedArray< 3, T > &	x,
		ads::FixedArray< 3, T > *	closestPoint
	)			`[related]`

Compute the signed distance and closest point from the 3-D point to the 2-simplex.

Parameters:

	s	is a 2-simplex (a triangle) in 3-D space.
	n	is the unit normal to the triangle face.
	x	is a Cartesian point in 3-D space.
	closestPoint	is the closest point on the simplex.

Returns:: the signed distance from the point to the simplex. The signed distance is defined above and below, but not to the side of the simplex. If the point is not above or below the simplex, return std::numeric_limits<T>::max().

template<typename T >

T computeSignedDistance	(	const Simplex< 2, ads::FixedArray< 3, T >, T > &	s,
		const ads::FixedArray< 3, T > &	x
	)			`[related]`

Compute the signed distance from the 3-D point to the 2-simplex.

Parameters:

	s	is a 2-simplex (a triangle) in 3-D space.
	x	is a Cartesian point in 3-D space.

Returns:: the signed distance from the point to the simplex. The signed distance is defined above and below, but not to the side of the simplex. If the point is not above or below the simplex, return std::numeric_limits<T>::max().

template<typename T >

T computeSignedDistance	(	const Simplex< 1, ads::FixedArray< 2, T >, T > &	s,
		const ads::FixedArray< 2, T > &	x,
		ads::FixedArray< 2, T > *	closestPoint
	)			`[related]`

Compute the signed distance and closest point from the 2-D point to the 1-simplex.

Parameters:

	s	is a 1-D simplex (a line segment) in 2-D space.
	x	is a Cartesian point in 2-D space.
	closestPoint	is the closest point on the simplex.

Returns:: the signed distance from the point to the simplex. The signed distance is defined above and below, but not to the side of the simplex. If the point is not above or below the simplex, return std::numeric_limits<T>::max().

template<typename T >

T computeSignedDistance	(	const Simplex< 1, ads::FixedArray< 2, T >, T > &	s,
		const ads::FixedArray< 2, T > &	x
	)			`[related]`

Compute the signed distance from the 2-D point to the 1-simplex.

Parameters:

	s	is a 1-D simplex (a line segment) in 2-D space.
	x	is a Cartesian point in 2-D space.

Returns:: the signed distance from the point to the simplex. The signed distance is defined above and below, but not to the side of the simplex. If the point is not above or below the simplex, return std::numeric_limits<T>::max().

template<int N, typename T >

T computeSignedDistance	(	const ads::FixedArray< N, T > &	p,
		const ads::FixedArray< N, T > &	n,
		const ads::FixedArray< N, T > &	x
	)			`[related]`

Compute the signed distance from the N-D point with normal to the N-D point.

Parameters:

	p	is an N-D Cartesian point.
	n	is a normal direction for the point.
	x	is an N-D Cartesian point.

Returns:: the signed distance. If 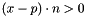$(x - p) \cdot n > 0$ , then the distance has positive sign.

Referenced by computeSignedDistance().

template<typename T >

T computeUnsignedDistance	(	const Simplex< 3, ads::FixedArray< 3, T >, T > &	s,
		const ads::FixedArray< 3, T > &	x
	)			`[related]`

Compute the unsigned distance from the 3-D point to the 3-D simplex.

Parameters:

	s	is a 3-D simplex (a tetrahedron) in 3-D space.
	x	is a 3-D Cartesian point.

Returns:: the unsigned distance from the point to the simplex. The distance is zero inside the simplex and positive outside.

References SegmentMath< N, T >::computeDistance(), and max().

template<typename T >

T computeUnsignedDistance	(	const Simplex< 2, ads::FixedArray< 2, T >, T > &	s,
		const ads::FixedArray< 2, T > &	x
	)			`[related]`

Compute the unsigned distance from the 2-D point to the 2-D simplex.

Parameters:

	s	is a 2-D simplex (a triangle) in 2-D space.
	x	is a 2-D Cartesian point.

Returns:: the unsigned distance from the point to the simplex. The distance is zero inside the simplex and positive outside.

References SegmentMath< N, T >::computeDistance(), and max().

template<typename T >

T computeUnsignedDistance	(	const Simplex< 1, ads::FixedArray< 1, T >, T > &	s,
		const ads::FixedArray< 1, T > &	x
	)			`[related]`

Compute the unsigned distance from the 1-D point to the 1-D simplex.

Parameters:

	s	is a 1-D simplex (an interval) in 1-D space.
	x	is a Cartesian point.

Returns:: the unsigned distance from the point to the simplex. The distance is zero inside the simplex and positive outside.

References SegmentMath< N, T >::computeDistance(), and max().

template<typename V , typename T >

bool hasFace	(	const Simplex< 3, V, T > &	simplex,
		const V &	x,
		const V &	y,
		const V &	z,
		int *	faceIndex
	)			`[related]`

Return true if the 3-simplex has the face specified by the three vertices.

Set the face index.

References Simplex< N, V, T >::computeOtherIndex(), Simplex< N, V, T >::getVertexIndex(), and Simplex< N, V, T >::hasFace().

template<int N, typename V , typename T >

bool hasFace	(	const Simplex< N, V, T > &	simplex,
		const typename Simplex< N, V, T >::Face &	face,
		int *	faceIndex
	)			`[related]`

Return true if the N-simplex has the specified (N-1)-face.

If true, set the face index.

References Simplex< N, V, T >::hasVertex(), and Simplex< N, V, T >::size().

Referenced by Simplex< N, V, T >::hasFace(), and SmrCell< SMR >::hasFace().

template<typename V , typename T >

bool haveSameOrientation	(	const Simplex< 2, V, T > &	x,
		const Simplex< 2, V, T > &	y
	)			`[related]`

Return true if the two simplices have the same orientation.

Precondition:: x and y must have the same vertices.

References Simplex< N, V, T >::hasVertex().

template<typename V , typename T >

bool haveSameOrientation	(	const Simplex< 1, V, T > &	x,
		const Simplex< 1, V, T > &	y
	)			`[related]`

Return true if the two simplices have the same orientation.

Precondition:: x and y must have the same vertices.

References Simplex< N, V, T >::hasVertex().

template<typename V , typename T >

bool haveSameOrientation	(	const Simplex< 0, V, T > &	x,
		const Simplex< 0, V, T > &	y
	)			`[related]`

Return true if the two simplices have the same orientation.

Precondition:: x and y must have the same vertices.

template<typename T >

bool isIn	(	const Simplex< 3, ads::FixedArray< 3, T >, T > &	s,
		const ads::FixedArray< 3, T > &	x
	)			`[related]`

Return true if the 3-D point is inside the 3-D simplex.

Parameters:

	s	is a 3-D simplex (a tetrahedran) in 3-D space with Cartesian points as vertices.
	x	is a point in 3-D Cartesian space.

Consider the supporting planes of the four faces. The point is in the simplex if and only if it has negative distance to each of the planes.

Returns:: true if the point is inside the simplex.

template<typename T >

bool isIn	(	const Simplex< 2, ads::FixedArray< 2, T >, T > &	s,
		const ads::FixedArray< 2, T > &	x
	)			`[related]`

Return true if the 2-D point is inside the 2-D simplex.

Parameters:

	s	is a 2-D simplex (a triangle) in 2-D space with Cartesian points as vertices.
	x	is a point in 2-D Cartesian space.

Consider the supporting lines of the three faces. The point is in the simplex if and only if it has negative distance to each of the lines.

Returns:: true if the point is inside the simplex.

template<typename T >

BEGIN_NAMESPACE_GEOM bool isIn	(	const Simplex< 1, ads::FixedArray< 1, T >, T > &	s,
		const ads::FixedArray< 1, T > &	x
	)			`[related]`

Return true if the 1-D point is inside the 1-D simplex.

Parameters:

	s	is a 1-D simplex (an interval) in 1-D space.
	x	is a point in 1-D Cartesian space.

Returns:: true if the point is inside the simplex.

template<int N, typename V , typename T >

bool operator==	(	const Simplex< N, V, T > &	x,
		const Simplex< N, V, T > &	y
	)			`[related]`

Return true if the vertices are given in the same order.

Note: This does not check if the vertices of x are an even permutation of the vertices of y.

References Simplex< N, V, T >::getVertices().

The documentation for this class was generated from the following files:

Simplex< N, V, T > Class Template Reference

Public Types

Public Member Functions

Related Functions

Detailed Description

template<int N, typename V, typename T = double> class Simplex< N, V, T >

Member Function Documentation

Friends And Related Function Documentation

template<int N, typename V, typename T = double>
class Simplex< N, V, T >