SimplexJac< N, T > Class Template Reference
Implements operations for the Jacobian matrix of a simplex. More...
#include <SimplexJac.h>
Public Types | |
| typedef T | Number |
| The number type. | |
|
typedef ads::FixedArray< N, Number > | Vertex |
| The class for a vertex. | |
|
typedef geom::Simplex< N, Vertex, Number > | Simplex |
| The simplex type. | |
|
typedef ads::SquareMatrix< N, Number > | Matrix |
| An NxN matrix. | |
Public Member Functions | |
Constructors etc. | |
| SimplexJac () | |
| Default constructor. Un-initialized memory. | |
| SimplexJac (const SimplexJac &other) | |
| Copy constructor. | |
| SimplexJac (const Simplex &s) | |
| Construct from a simplex. | |
| SimplexJac & | operator= (const SimplexJac &other) |
| Assignment operator. | |
| ~SimplexJac () | |
| Trivial destructor. | |
Accessors | |
| const Matrix & | getMatrix () const |
| Return a const reference to the Jacobian matrix. | |
|
const ads::FixedArray< N, Matrix > & | getGradientMatrix () const |
| Return a const reference to the gradient of the Jacobian matrix. | |
| Number | getDeterminant () const |
| Return the determinant of the Jacobian matrix. | |
| const Vertex & | getGradientDeterminant () const |
| Return a const reference to the gradient of the determinant of the Jacobian matrix. | |
| Number | computeContent () const |
| Return the content (hypervolume) of the simplex. | |
| void | computeGradientContent (Vertex *grad) const |
| Calculate the gradient of the content (hypervolume) of the simplex. | |
| Vertex | computeGradientContent () const |
| Return the gradient of the content (hypervolume) of the simplex. | |
Manipulators | |
| void | setFunction (const Simplex &s) |
| Set the vertices. Calculate the Jacobian matrix and determinant. | |
| void | set (const Simplex &s) |
| Set the vertices. Calculate the Jacobian matrix and the determinant and its gradient. | |
| void | setFunction (const geom::Simplex< N, ads::FixedArray< N+1, Number >, Number > &s) |
| Set the vertices. Calculate the Jacobian matrix and determinant. | |
| void | set (const geom::Simplex< N, ads::FixedArray< N+1, Number >, Number > &s) |
| Set the vertices. Calculate the Jacobian matrix and the determinant and its gradient. | |
Detailed Description
template<int N, typename T = double>
class SimplexJac< N, T >
Implements operations for the Jacobian matrix of a simplex.
- Parameters:
-
N is the dimension. T is the number type. By default it is double.
The Jacobian Matrix
Consider a simplex 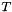 with vertices
with vertices 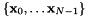 . We call this the physical simplex. The identity simplex
. We call this the physical simplex. The identity simplex 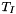 may be mapped to the physical simplex
may be mapped to the physical simplex 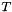 by an affine transformation and a translation.
by an affine transformation and a translation.
![\[ T = S T_I + \mathbf{x}_0 \]](form_194.png)
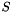 is the Jacobian matrix of the transformation.
is the Jacobian matrix of the transformation.
In 2-D, the identity triangle has vertices: 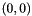 ,
, 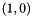 and
and 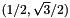 . In 3-D, the identity tetrahedron has vertices:
. In 3-D, the identity tetrahedron has vertices: 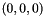 ,
, 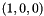 ,
, 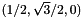 and
and 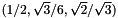 .
.
The logical simplex, 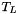 is the simplex whose vertices are the origin and unit displacements in each coordinate direction. In 2-D, the logical triangle has vertices:
is the simplex whose vertices are the origin and unit displacements in each coordinate direction. In 2-D, the logical triangle has vertices: 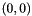 ,
, 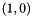 and
and 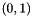 . In 3-D, the logical tetrahedron has vertices:
. In 3-D, the logical tetrahedron has vertices: 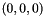 ,
, 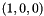 ,
, 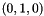 ,
, 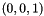 . It is easy to map the logical simplex to the physical simplex.
. It is easy to map the logical simplex to the physical simplex.
![\[ T = A T_L + \mathbf{x}_0 \]](form_207.png)
The columns of 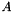 are the displacements of the vertices from the first vertex
are the displacements of the vertices from the first vertex 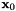 . In 3-D, this is
. In 3-D, this is
![\[ A = \left( \begin{array}{ccc} x_1 - x_0 & x_2 - x_0 & x_3 - x_0 \\ y_1 - y_0 & y_2 - y_0 & y_3 - y_0 \\ z_1 - z_0 & z_2 - z_0 & z_3 - z_0 \end{array} \right). \]](form_210.png)
It is also easy to map the logical simplex to the identity simplex.
![\[ T_I = W T_L \]](form_211.png)
The columns of 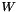 are the vertices of
are the vertices of 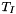 . In 3-D, this is
. In 3-D, this is
![\[ W = \left( \begin{array}{ccc} 1 & 1/2 & 1/2 \\ 0 & \sqrt{3} / 2 & \sqrt{3} / 6 \\ 0 & 0 & \sqrt{2} / \sqrt{3} \end{array} \right). \]](form_213.png)
By combining the former transformation with the inverse of the latter, we can map the identity simplex to the physical simplex.
![\[ T = A W^{-1} T_I + \mathbf{x}_0 \]](form_214.png)
The Jacobian matrix of the transformation is 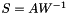 .
.
Usage
Construct a SimplexJac with the default constructor or from a SimplexJac::Simplex.
typedef geom::SimplexJac<3> TetJac; typedef TetJac::Vertex Vertex; typedef TetJac::Simplex Tetrahedron; // Default constructor. TetJac tet;
// The identity tetrahedron. Tetrahedron t(Vertex(0, 0, 0), Vertex(1, 0, 0), Vertex(1./2, std::sqrt(3.)/2, 0), Vertex(1./2, std::sqrt(3.)/6, std::sqrt(2./3.))); TetJac tet(t);
The Simplex constructor calls set() to enable evaluation of the determinant, the content and their gradients.
To evaluate the determinant or the content of the simplex, first call setFunction() to set the Jacobian matrix and then use the getDeterminant() and computeContent() member functions.
tet.setFunction(t); std::cout << "Identity tetrahedron:\n" << "determinant = " << tet.getDeterminant() << "\nvolume = " << tet.computeContent() << '\n';
To evaluate the determinant and content and/or their gradients, first call set() to set the Jacobian matrix and its gradient. Then use the member functions to access the appropriate qantities.
tet.set(t); std::cout << "Identity tetrahedron:\n" << "determinant = " << tet.getDeterminant() << "\ngrad determinant = " << tet.getGradientDeterminant() << "\nvolume = " << tet.computeContent() << "\ngrad volume = " << tet.computeGradientContent() << '\n';
Member Function Documentation
| void SimplexJac< N, T >::set | ( | const geom::Simplex< N, ads::FixedArray< N+1, Number >, Number > & | s | ) |
Set the vertices. Calculate the Jacobian matrix and the determinant and its gradient.
This first projects the simplex to N-D and then call the above set().
| void SimplexJac< N, T >::setFunction | ( | const geom::Simplex< N, ads::FixedArray< N+1, Number >, Number > & | s | ) |
Set the vertices. Calculate the Jacobian matrix and determinant.
This first projects the simplex to N-D and then call the above setFunction().
The documentation for this class was generated from the following file:
Generated on Thu Jun 30 02:14:58 2016 for Computational Geometry Package by
 1.6.3
1.6.3