Orientation Tests

Functions
template<typename T >
T	computeOrientationDeterminant (const ads::FixedArray< 2, T > &a, const ads::FixedArray< 2, T > &b, const ads::FixedArray< 2, T > &c)
	Compute the orientation determinant.
template<typename T >
T	computeInCircleDeterminant (const ads::FixedArray< 2, T > &a, const ads::FixedArray< 2, T > &b, const ads::FixedArray< 2, T > &c, const ads::FixedArray< 2, T > &d)
	Compute the in-circle determinant.
template<typename T >
bool	isInCircle (const ads::FixedArray< 2, T > &a, const ads::FixedArray< 2, T > &b, const ads::FixedArray< 2, T > &c, const ads::FixedArray< 2, T > &d)
	Return true if `d` is inside the circle with `a`, `b`, and `c` on its boundary.

Detailed Description

Function Documentation

template<typename T >

T computeInCircleDeterminant	(	const ads::FixedArray< 2, T > &	a,
		const ads::FixedArray< 2, T > &	b,
		const ads::FixedArray< 2, T > &	c,
		const ads::FixedArray< 2, T > &	d
	)			`[inline]`

Compute the in-circle determinant.

Return the determinant of:

$\Gamma = \left[ \begin{array}{cccc} 1 & a_0 & a_1 & a_2\\ 1 & b_0 & b_1 & b_2\\ 1 & c_0 & c_1 & c_2\\ 1 & d_0 & d_1 & d_2 \end{array} \right]$

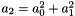where $a_2 = a_0^2 + a_1^2$ . Point d lies inside the circle passing through a, b, and c if and only if 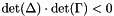$\mathrm{det}(\Delta) \cdot \mathrm{det}(\Gamma) < 0$ .

See Geometry and Topology for Mesh Generation.

Referenced by isInCircle().

template<typename T >

T computeOrientationDeterminant	(	const ads::FixedArray< 2, T > &	a,
		const ads::FixedArray< 2, T > &	b,
		const ads::FixedArray< 2, T > &	c
	)			`[inline]`

Compute the orientation determinant.

Return the determinant of:

$\Delta = \left[ \begin{array}{ccc} 1 & a_0 & a_1 \\ 1 & b_0 & b_1 \\ 1 & c_0 & c_1 \end{array} \right]$

It is positive for a left turn, negative for a right turn, and zero if the points are colinear.

See Geometry and Topology for Mesh Generation.

Referenced by isInCircle().

template<typename T >

bool isInCircle	(	const ads::FixedArray< 2, T > &	a,
		const ads::FixedArray< 2, T > &	b,
		const ads::FixedArray< 2, T > &	c,
		const ads::FixedArray< 2, T > &	d
	)			`[inline]`

Return true if d is inside the circle with a, b, and c on its boundary.

Point d lies inside the circle passing through a, b, and c if and only if 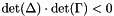$\mathrm{det}(\Delta) \cdot \mathrm{det}(\Gamma) < 0$ .

See Geometry and Topology for Mesh Generation.

References computeInCircleDeterminant(), and computeOrientationDeterminant().

Orientation Tests

Functions

Detailed Description

Function Documentation