Multiple Range Queries

Single versus Multiple Queries

To the best of my knowledge, there has not been any previously published work addressing the issue of doing a set of orthogonal range queries. There has been a great deal of work on doing single queries. However, there are no previously introduced algorithms that can perform a set of Q queries in less time than the product of Q and the time of a single query. In this section we will introduce an algorithm for doing multiple 1-D range queries. In the following section we will extend the algorithm to higher dimensions.

Sorted Key and Sorted Ranges with Forward Searching

Previously we sorted the file by its keys. The purpose of this was to enable us to use a binary search to find a record. The binary search requires a random access iterator to the records. That is, it can access any record of the file in constant time. Typically this means that the records are stored in an array. Now we introduce a data structure that stores its data in sorted order, but need only provide a forward iterator. A container of this type must provide the attribute begin, which points to the first element and the attribute end, which points to one past the last element. A forward iterator must support the following operations.

dereference

*iter returns the element pointed to by iter.

increment

++iter moves iter to the next element.

In addition, the forward iterator supports assignment and equality tests. All of the containers in the C++ STL library satisfy these criteria. (See Generic programming and the STL: using and extending the C++ Standard Template Library for a description of containers, iterators and the C++ STL library.)

We will store pointers to the records in such a container, sorted by key. Likewise for the ranges, sorted by the lower end of each range. Below is the algorithm for doing a set of range queries. The MRQ prefix stands for multiple range queries.

MRQ_sorted_key_sorted_range(records, ranges):
  initialize(records)
  range_iter = ranges.begin
  while range_iter  ranges.end:
    included_records = RQ_forward_search(records, *iter)
    // Do something with included_records
    ++range_iter

initialize(container):
  container.first_in_range = container.begin

RQ_forward_search(records, range):
1  included_records = 
2  while (records.first_in_range  records.end and (*records.first_in_range).key < range.min):
3    ++records.first_in_range
4  iter = records.first_in_range
5  while (*iter).key  range.max:
6    included_records += iter
7    ++iter
8  return included_records

Let there be N elements and Q queries. Let T be the total number of records in query ranges, counting multiplicities. The computational complexity of doing a set of range queries is 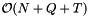. Iterating over the query ranges introduces the 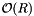term. Searching for the beginning of each range accounts for 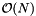. This occurs on lines 2 and 3 of RQ_forward_search(). Finally, collecting the included records (lines 4-7) accounts for the 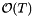term. To match the previous notation, let I be the average number of records in a query. The average cost of a single query is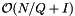

The preprocessing time for making the data structure is 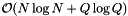because the records and query ranges must be sorted. If the records and query ranges change by small amounts, the reprocessing time is 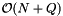because the records and query ranges can be resorted with an insertion sort. The storage requirement is linear in the number of records and query ranges.