SimplexAdjJac< N, T > Class Template Reference
Implements operations for the adjoint Jacobian matrix of a simplex. More...
#include <SimplexAdjJac.h>
Public Types | |
| typedef T | Number |
| The number type. | |
|
typedef ads::SquareMatrix< N, Number > | Matrix |
| An NxN matrix. | |
Public Member Functions | |
Constructors etc. | |
| SimplexAdjJac () | |
| Default constructor. Un-initialized memory. | |
| SimplexAdjJac (const SimplexAdjJac &other) | |
| Copy constructor. | |
| SimplexAdjJac (const Matrix &jacobian) | |
| Construct from the Jacobian matrix. | |
| SimplexAdjJac & | operator= (const SimplexAdjJac &other) |
| Assignment operator. | |
| ~SimplexAdjJac () | |
| Trivial destructor. | |
Accessors | |
| const Matrix & | getMatrix () const |
| Return a const reference to the adjoint Jacobian matrix. | |
|
const ads::FixedArray< N, Matrix > & | getGradientMatrix () const |
| Return a const reference to the gradient of the adjoint Jacobian matrix. | |
Manipulators | |
| void | setFunction (const Matrix &jacobian) |
| Calculate the adjoint Jacobian matrix. | |
| void | set (const Matrix &jacobian) |
| Calculate the adjoint Jacobian matrix and its gradient. | |
Detailed Description
template<int N, typename T = double>
class SimplexAdjJac< N, T >
Implements operations for the adjoint Jacobian matrix of a simplex.
- Parameters:
-
N is the dimension. T is the number type. By default it is double.
The Adjoint of a Matrix
Consult the documentation of geom::SimplexJac for information on the Jacobian matrix of a simplex. This class implements operations on the adjoint of this matrix. In this context, the adjoint is the scaled inverse of a matrix. The adjoint of a non-singular matrix 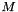 is
is 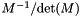 . For the general case, we have:
. For the general case, we have:
![\[ M \cdot \mathrm{adj}(M) = \mathrm{det}(M) I \]](form_182.png)
where 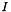 is the identity matrix.
is the identity matrix.
The adjoint of the Jacobian matrix of a simplex is used in the condition number quality metric. (See geom::SimplexCondNum and geom::SimplexModCondNum.)
Usage
Make a SimplexAdjJac by using the default constructor or the Matrix constructor.
typedef geom::SimplexJac<3> TetJac; typedef geom::SimplexAdjJac<3> TetAdjJac; typedef TetJac::Vertex Vertex; typedef TetJac::Simplex Tetrahedron; // Default constructor. TetAdjJac adjoint;
// Identity tetrahedron Tetrahedron t(Vertex(0, 0, 0), Vertex(1, 0, 0), Vertex(1./2, std::sqrt(3.)/2, 0), Vertex(1./2, std::sqrt(3.)/6, std::sqrt(2./3.))); // The Jacobian matrix. TetJac jacobian(t); // The adjoint of the Jacobian matrix. TetAdjJac adjoint(jacobian.getMatrix());
The latter constructor calls the set() member function.
To evaluate the adjoint of the Jacobian, first call the setFunction() manipulator and then use the getMatrix() accessor.
adjoint.setFunction(jacobian.getMatrix()); std::cout << "Adjoint = \n" << adjoint.getMatrix() << '\n';
To evaluate the adjoint of the Jacobian and its gradient, first call the set() manipulator and then use the getMatrix() and getGradientMatrix() accessors.
adjoint.set(jacobian.getMatrix()); std::cout << "Adjoint = \n" << adjoint.getMatrix() << "\nGradient of adjoint = \n" << adjoint.getGradientMatrix() << '\n';
The documentation for this class was generated from the following file:
Generated on Thu Jun 30 02:14:58 2016 for Computational Geometry Package by
 1.6.3
1.6.3