interp_extrap.h File Reference
Interpolation/extrapolation for grids. More...
#include "../defs.h"#include "../../ads/array/Array.h"#include "ArrayContainer.h"#include "ArrayIndexing.h"#include "Array.ipp"#include "Array1.h"#include <iosfwd>#include "../kernel/BBox.h"#include <limits>#include "RegularGrid.ipp"Go to the source code of this file.
Functions | |
| template<int N, int M, typename T > | |
| BEGIN_NAMESPACE_NUMERICAL void | grid_interp_extrap (const int num_points, T values[], const T positions[], const T default_values[M], const int extents[N], const T domain[2 *N], const T *distance, const T *fields[M]) |
| Grid interpolation/extrapolation for a set of points. | |
| template<int N, int M, typename T > | |
| void | grid_interp_extrap (const int num_points, T values[], const T positions[], const T default_values[M], const int extents[N], const T domain[2 *N], const T *distance, const T *fields) |
| Grid interpolation/extrapolation for a set of points. | |
Detailed Description
Interpolation/extrapolation for grids.
Function Documentation
| void grid_interp_extrap | ( | const int | num_points, | |
| T | values[], | |||
| const T | positions[], | |||
| const T | default_values[M], | |||
| const int | extents[N], | |||
| const T | domain[2 *N], | |||
| const T * | distance, | |||
| const T * | fields | |||
| ) | [inline] |
Grid interpolation/extrapolation for a set of points.
- Parameters:
-
num_points is the number of points at which to interpolate/extrapolate the fields. values is an array of length M*num_points. It will be set to the interpolated/extrapolated fields. For M = 2 the layout ispoint_0_field_0 point_0_field_1 point_1_field_0 point_1_field_1 ...
positions is an array of length N*num_points. It holds the positions of the points in Cartesian coordinates. In 3-D the layout ispoint_0_x point_0_y point_0_z point_1_x point_1_y point_1_z ...
default_values are the default values for the fields. If there are no nearby grid points with known values for a given point, the field values will be set to these default values. The "nearby" grid points are the 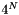 grid points that surround the point.
grid points that surround the point.extents are the extents of the grid. domain is the Cartesian domain of the grid. In 3-D, the format is { xmin, ymin, zmin, xmax, ymax, zmax }distance is the distance array. It has size extents[0] * ... * extents[N-1]
The field values are known at grid points with non-negative distance and unknown at grid points with negative distance. The first coordinate varies fastest. For an X by Y grid in 2-D the layout is
distance(0,0) distance(1,0) ... distance(X-1,0) distance(0,1) distance(1,1) ... distance(X-1,1) ... distance(0,Y-1) distance(1,Y-1) ... distance(X-1,Y-1)
fields is the array of the vector fields. The Mfields for for a grid point are contiguous in memory.
Template Parameters:
Nis the dimension. (1-D, 2-D and 3-D is supported.)Mis the number of fields.Tis the number type.
Explicitly specify the dimension and the number of fields in the function call as these cannot be deduced from the arguments, i.e. use grid_interp_extrap<3,2>(...) for a 3-D problem with 2 fields.
Example usage: 3-D with one field. (N = 3, M = 1, T = double)
const int num_points = ...; double values[ num_points ]; double positions[ 3 * num_points ]; // Set the positions. ... const double default_values[1] = { 0 }; // A 100 x 100 x 100 grid. const int extents[3] = { 100, 100, 100 }; // The grid spans the unit cube. const double domain[6] = { 0, 0, 0, 1, 1, 1 }; double distance[1000000]; double fields[1000000]; // Set the distance and field values. ... numerical::grid_interp_extrap<3,1>(num_points, values, positions, default_values, extents, domain, distance, fields);
| BEGIN_NAMESPACE_NUMERICAL void grid_interp_extrap | ( | const int | num_points, | |
| T | values[], | |||
| const T | positions[], | |||
| const T | default_values[M], | |||
| const int | extents[N], | |||
| const T | domain[2 *N], | |||
| const T * | distance, | |||
| const T * | fields[M] | |||
| ) | [inline] |
Grid interpolation/extrapolation for a set of points.
- Parameters:
-
num_points is the number of points at which to interpolate/extrapolate the fields. values is an array of length M*num_points. It will be set to the interpolated/extrapolated fields. For M = 2 the layout ispoint_0_field_0 point_0_field_1 point_1_field_0 point_1_field_1 ...
positions is an array of length N*num_points. It holds the positions of the points in Cartesian coordinates. In 3-D the layout ispoint_0_x point_0_y point_0_z point_1_x point_1_y point_1_z ...
default_values are the default values for the fields. If there are no nearby grid points with known values for a given point, the field values will be set to these default values. The "nearby" grid points are the 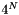 grid points that surround the point.
grid points that surround the point.extents are the extents of the grid. domain is the Cartesian domain of the grid. In 3-D, the format is { xmin, ymin, zmin, xmax, ymax, zmax }distance is the distance array. It has size extents[0] * ... * extents[N-1]
The field values are known at grid points with non-negative distance and unknown at grid points with negative distance. The first coordinate varies fastest. For an X by Y grid in 2-D the layout is
distance(0,0) distance(1,0) ... distance(X-1,0) distance(0,1) distance(1,1) ... distance(X-1,1) ... distance(0,Y-1) distance(1,Y-1) ... distance(X-1,Y-1)
fields is an array of the M field arrays. Each field array has the same size and layout as the distance array.
Template Parameters:
Nis the dimension. (1-D, 2-D and 3-D is supported.)Mis the number of fields.Tis the number type.
Explicitly specify the dimension and the number of fields in the function call as these cannot be deduced from the arguments, i.e. use grid_interp_extrap<3,2>(...) for a 3-D problem with 2 fields.
The field values for a point are only interpolated/extrapolated if there are two grid points on every side of the point. (In 1-D, the point must be surrounded by 4 grid points. In 3-D, the point must be surrounded by 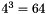 grid points.) Otherwise the values are left unchanged. This enables one to use multiple grids to interpolate the values. Just call the function once for each grid. The
grid points.) Otherwise the values are left unchanged. This enables one to use multiple grids to interpolate the values. Just call the function once for each grid. The values array will accumulate the results. If there are overlapping grids of different resolutions, start with the coarsest grids and end with the finest. This way interpolation/extrapolation results from the finer grids may overwrite results from the coarser grids.
Example usage: 3-D with one field. (N = 3, M = 1, T = double)
const int num_points = ...; double values[ num_points ]; double positions[ 3 * num_points ]; // Set the positions. ... const double default_values[1] = { 0 }; // A 100 x 100 x 100 grid. const int extents[3] = { 100, 100, 100 }; // The grid spans the unit cube. const double domain[6] = { 0, 0, 0, 1, 1, 1 }; double distance[1000000]; double field[1000000]; // Set the distance and field values. ... const double* fields[1] = { field }; numerical::grid_interp_extrap<3,1>(num_points, values, positions, default_values, extents, domain, distance, fields);
The figure below shows the 16 possibilities for 1-D interpolation/extrapolation. The graph at the top shows four grid points that sample a function and an interpolation/extrapolation point marked with an x. Solid/hollow points indicate that the value is/isn't known.
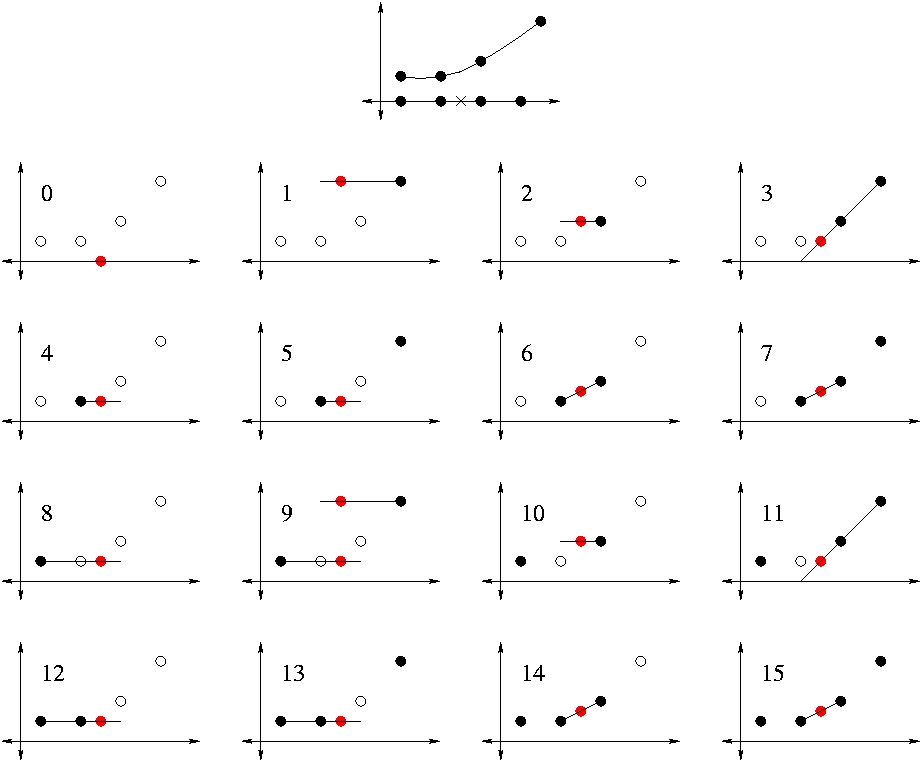
1-D Interpolation/Extrapolation
The cases show linear interpolation, linear extrapolation and constant extrapolation. In case 0, no grid points have known values. Thus the value is set to the user-defined default. In case 9, constant value extrapolation is perform from the closer known grid point. In this example the interpolation/extrapolation point is equidistant from the two known grid points so we show both extrapolations.
In 2-D and 3-D, the interpolation/extrapolation is performed one dimension at a time. If there are any known grid points along a dimension, then the interpolated/extrapolated value is known; otherwise it is unknown.
Below is a diagram illustrating the process in 2-D. The interpolation/extrapolation point, marked with a red x, lies on a curve. Grid points with positive/negative distance from the curve have known/unknown field values. Again, solid/hollow grid points indicate known/unkown values.
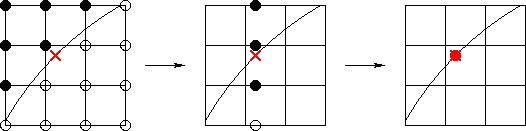
2-D Interpolation/Extrapolation
In the first step, we interpolate/extrapolate in the x direction.
- For the top row we use linear interpolation between the second and third grid points.
- For the second row we use linear extrapolation from the first and second grid points.
- For the third row we use constant extrapolation from the first grid point.
- For the final row no grid points are known.
For the second step we interpolate/extrapolate in the y direction. In this case we use linear interpolation between the second and third grid points to determine the field value.
Generated on Thu Jun 30 02:15:00 2016 for Numerical Algorithms Package by
 1.6.3
1.6.3