An Overview of the Simplicial Mesh Package.

Introduction.

This package contains a suite of hill-climbing methods for mesh optimization. That is, each method sweeps over the mesh, investigating local changes. If the proposed transformation locally improves the quality of the mesh, then the change is accepted. The local changes are comprised of geometric transformations (moving vertices) and topological transformations (changing the connectivities).

There are also refinement and coarsening capabilities. Refinement is done with edge splitting; coarsening with edge collapse. These are used for error control and efficiency, respectively.

A feature-based representation of the boundary is used in many of the mesh optimization algorithms. For a 3-D mesh, the boundary is represented as a triangle mesh that has surface features, edge features, and corner features. Sharp edges and corners are preserved as nodes are moved and cells are modified.

One can use either an explicit (parametric) or an implicit (level set) description of the boundary. The explicit description is useful for moving points along the boundary. For the level set description, the boundary is stored in a bounding box tree, which supports efficient minimum distance queries. In this manner the distance to the boundary and the closest point on the boundary may be determined for any point in space. This representation of the boundary enables moving nodes onto the boundary.

Algorithms.

The following algorithms are currently implemented in 2-D and 3-D.

• Algebraic quality metrics. These metrics are functions of the Jacobian matrix of the mapping from the equilateral simplex to the physical simplex. They are differentiable and sensitive to all types of degeneracies.
• Geometric optimization of vertex positions. A vertex is moved to optimize the quality of the incident simplices. Boundary vertices are moved along the feature-based description of the boundary. Alterntively, boundary vertices may be optimized subject to a constant content constraint or may be optimized and then constrained to remain on a specified curve/surface.
• Topological optimization. Local transformations (edge flips in 2-D, edge removal and face removal in 3-D) are applied in a hill-climbing strategy.
• Refinement. One can refine a set of cells or refine the mesh based on a maximum allowed edge length function. If a cell is targeted for refinement, its longest edge will be split. However, only mutual longest edges are allowed to be split. This means that adjacent cells may need to be (recursively) refined before the targeted cell is refined.
• Coarsening. The mesh is coarsened by removing cells through edge collapse. One can coarsen the mesh by collapsing edges for a set of cells or by specifying a minimum allowed edge length function. There are user-defined parameters for controlling the quality of the mesh while performing coarsening.
• Conversion of a simplicial mesh to a level set function. There is a data structure that allows a mesh to be treated as a distance function or a closest point function. It combines a lower-upper bound query on a bounding box tree with distance and closest point calculations to the elements of the mesh.
• Mesh transfer. There is a robust mesh transfer algorithm for transfering fields from one simplicial mesh to another. Given a point and a field, the algorithm first determines the simplex to which the point has minimum distance. The distance could be negative or positive depending on whether the point is inside or outside the simplex. Then one can perform interpolation or extrapolation with the fields defined in the simplex. 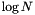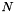The minimum distance calculation uses a lower-upper bound query on a bounding box tree which has expected complexity where is the number of simplices.

Data Structures.

There are mesh data structures for both static topology and dynamic topology. (See the data structures page for details and comparisons.) The static topology data structures (geom::IndSimpSet and geom::IndSimpSetIncAdj) are used in geometric optimization, the level set capability, and boundary description. The dynamic topology data structure (geom::SimpMeshRed) is used in topological optimization, refinement and coarsening. The data structures are light-weight, and flexible. The space dimension, simplex dimension (triangle, tetrahedron, etc.), as well as the node and element types are specified as template parameters. We anticipate that these data structures will be sufficient for future algorithmic development.

The boundary manifold data structures are geom::PointsOnManifold<3,2,1,T> and geom::PointsOnManifold<N,1,1,T>, for 3-D and 2-D, respectively. They capture the features of the boundary. In 3-D, the boundary has surface, edge, and corner features. Nodes may be moved along the boundary, inserted in the boundary, or deleted from the boundary.

Future Work.

• Add more quality functions.
• Combine geometric optimization with topological optimization to form more general transformations for the hill-climbing optimization approach.
• Make refinement more efficient by avoiding deep recursion.