Simplicial Mesh Package

Simple Topological Transformations

In 3-D, local topological transformations replace a set of tetrahedra with a different set that fills the same domain. (On the boundary they may fill only approximately the same domain.)

A 2-3 flip removes a face and adds a new edge. The inverse is a 3-2 flip. Two boundary faces are replaced in a 2-2 flip. The faces should be approximately co-planar.

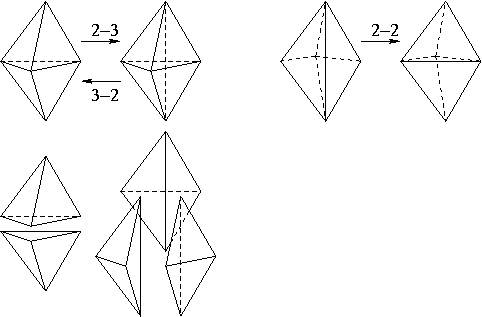
Composite Topological Transformations

We have been implementing the algorithms presented in ``Two Discrete Optimization Algorithms for the Topological Improvement of Tetrahedral Meshes'' by Jonathan Shewchuk. He presents two composite topological operations: edge removal and multi-face removal. These are more general than simple flips.

Edge removal and multi-face removal operations can be represented by sequences of 2-3, 3-2, 2-2 and 4-4 flips. Although a given composite operation may improve the mesh, some of its individual flips may temporarily reduce the quality. (They may even invert elements.) Thus using such composite operations is likely to produce better results than using only simple topological changes.

Edge Removal for Interior Edges

For interior edges, edge removal replaces 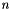tetrahedra with 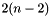tetrahedra. This includes 3-2, 4-4, 5-6 and other flips.

The ring of vertices around the edge are triangulated using Klincsek's algorithm to produce an optimal triangulation.

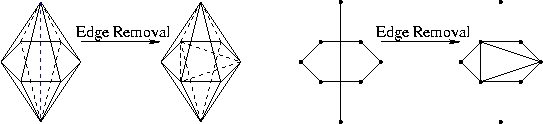
Edge removal that produces a 6-8 flip.

Edge Removal for Boundary Edges

For boundary edges, an edge is swapped on two approximately co-planar boundary faces. It replaces 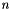tetrahedra with 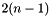tetrahedra. This includes 2-2, 3-4, 4-6 and other flips.

Boundary edge removal changes the volume of the mesh. It is performed only if the surface is approximately planar. In our implementation, boundary edges may be removed if the angle between the normals of the two adjacent boundary faces is less than a user specified constant.

Edge removal that produces a 4-6 flip. An edge removal that changes the volume of the mesh.

We have implemented edge removal for interior and boundary edges.

Multi-Face Removal

Multi-face removal is the inverse of edge removal. It removes the faces that are sandwiched between two vertices and inserts an edge between the vertices. The optimal set of faces is determined with Shewchuk's algorithm.

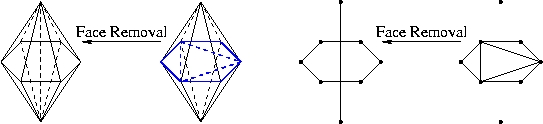
Face removal that produces an 8-6 flip.

Currently in our implementation only one or two faces can be removed by face removal. We will implement the general multi-face removal algorithm.

Topological Optimization

We apply local topological transformations in a hill-climbing method. We can use this to find a (local) maximum quality mesh.

One can repeatedly sweep over all the edges and faces, applying edge and face removal. However this is very inefficient. A better approach is to keep track of the edges and faces upon which local topological changes could possibly improve the mesh.

We maintain a set of active tetrahedra. Tetrahedra are added to the active set upon insertion in the mesh. Tetrahedra are removed from the set when they are removed from the mesh or when it is determined that edge or face removal on its edges and faces will not improve the mesh.

Data Structures

The geom::SimpMeshRed class is a reduced representation of a simplicial mesh.

Use the classs by including the file mesh/simplicial.h or by including mesh.h.