Orthant Arithmetic
Orthant Numbering
The 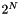 orthants are numbered from 0 to
orthants are numbered from 0 to 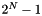 . The following figure and table show this numbering for the 2-D case of quadrants.
. The following figure and table show this numbering for the 2-D case of quadrants.

The quadrants.
| Number | y | x | Binary Number |
|---|---|---|---|
| 0 | - | - | 00 |
| 1 | - | + | 01 |
| 2 | + | - | 10 |
| 3 | + | + | 11 |
Note that the origin is in the lower left corner. In computer graphics, one often places the origin in the upper left corner so that row numbering starts at the top of the screen. We instead use the convention that is more familiar in geometry and physics.
The table below lists octant numbering.
| Number | z | y | x | Binary Number |
|---|---|---|---|---|
| 0 | - | - | - | 000 |
| 1 | - | - | + | 001 |
| 2 | - | + | - | 010 |
| 3 | - | + | + | 011 |
| 4 | + | - | - | 100 |
| 5 | + | - | + | 101 |
| 6 | + | + | - | 110 |
| 7 | + | + | + | 111 |
This is a nifty numbering system because the binary representation of the orthant encodes the N coordinate directions (0 for negative and 1 for positive). Specifically, the 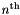 bit (starting with the least significant bit) encodes the direction for the
bit (starting with the least significant bit) encodes the direction for the 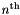 coordinate. Let the coordinates be labeled from 0 to N - 1. If i is the orthant number, the we can get the direction bit (0 or 1) for the
coordinate. Let the coordinates be labeled from 0 to N - 1. If i is the orthant number, the we can get the direction bit (0 or 1) for the 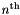 coordinate with a shift and a modulus.
coordinate with a shift and a modulus.
(i >> n) % 2
It easy to transform this to a direction sign (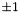 ).
).
((i >> n) % 2) * 2 - 1
By the way, you can write express multiplication and division by a power of 2 as left or right shifting. x * 2 is the same as x << 1. Any reasonable compiler will generate the same (efficient) code regardless of whether you use the former or latter method.
Directions
In N-D space there are 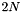 signed coordinate directions. We label these with integers from 0 to
signed coordinate directions. We label these with integers from 0 to 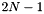 . In the figure and table below we show the direction numbering in 2-D.
. In the figure and table below we show the direction numbering in 2-D.

The direction numbering in 2-D.
| Number | Direction |
|---|---|
| 0 | -x |
| 1 | +x |
| 2 | -y |
| 3 | +y |
The next table gives the direction numbering in 3-D.
| Number | Direction |
|---|---|
| 0 | -x |
| 1 | +x |
| 2 | -y |
| 3 | +y |
| 4 | -z |
| 5 | +z |
This is a nifty numbering scheme because is easy to extract the coordinate number and the coordinate direction. For direction i the former is i / 2 and the latter is i % 2. (Here we use 0 and 1 to indicate negative and positive.)
Generated on Thu Jun 30 02:14:58 2016 for Computational Geometry Package by
 1.6.3
1.6.3