The Five Essential Ingredients of Mesh Optimization
There are five essential ingredients to any program of mesh optimization:
- Element quality metric.
- Geometric optimization.
- Topological optimization.
- Element size control.
- Boundary description.
Element Quality
The quality of a mesh is measured in terms of the quality of its elements. Thus one needs a metric for assessing element quality. Simply put, an element that is close to the ideal shape (perhaps an equilateral tetrahedron) has good quality and an element that is far from the ideal shape has poor quality. Below are poor quality tetrahedra that are nearly co-linear or co-planar.
Poor quality tetrahedra.
The positions of the nodes defines the geometry of a mesh. If the nodes are not well-spaced, then it is not possible to connect them to make quality elements. Any mesh optimization program must be able to improve the geometry of the mesh.
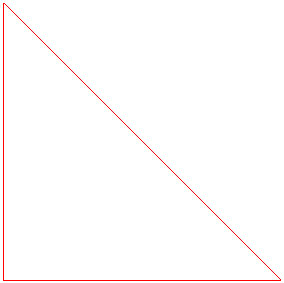
Below is a mesh with good geometry. The nodes are connected to form quality triangles.

Next consider a mesh with bad geometry. Note that there is no way of forming quality elements with these node positions. One is forced to make skinny triangles along the bottom of the square.

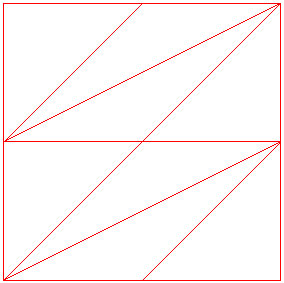
Topology
The connectivity of the nodes to form elements defines the topology of a mesh. If a mesh has poor topology, then no course of geometry optimization alone could yield a high quality mesh. Below is a mesh with good topology and relatively poor topology.

Element Size
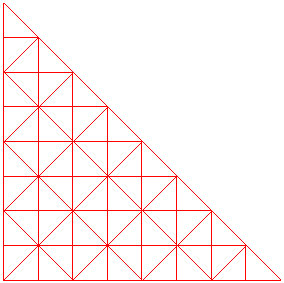
For most applications, it is not sufficient that a mesh have well-shaped elements. the elements must also satisy size requirements. For finite element applications, elements that are too large increase the error and elements that are too small increase the cost of the computation.
Consider the following three meshes. In terms of element shape, they have the same quality. However, the meshes are clearly not equivalent.
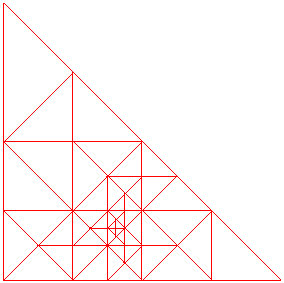
Boundary
Finally, consider the following mesh of the circle.
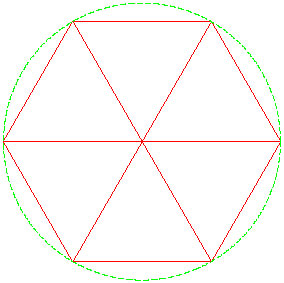
If we were to refine the triangles, it would no longer be the mesh of a circle; it would be the mesh of a hexagon.
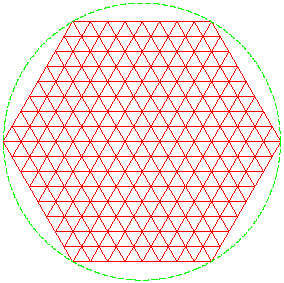
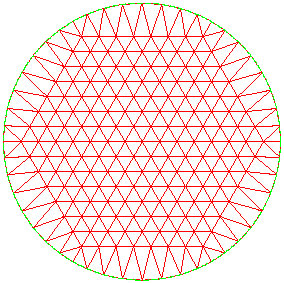
It is apparent that if we change the mesh, we need a means of keeping the boundary nodes on the boundary curve.
Generated on Thu Jun 30 02:14:57 2016 for Computational Geometry Package by
 1.6.3
1.6.3