Bent Cube Example
We start with a mesh of the unit cube. The edges of the tetrahedra have lengths close to 0.1. In the figures below, we show the modified condition number of the elements.
cp ../../../data/geom/mesh/33/cube_1_1_1_0.1.txt mesh.txt
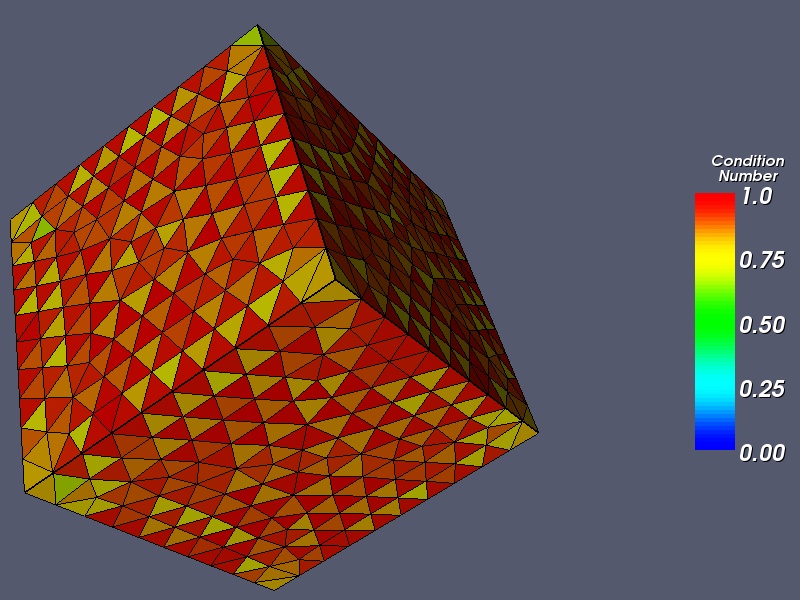
The initial mesh of the cube. The minimum modified condition number is 0.58; the mean is 0.86.
x = x y = y z = z + 0.75 - 1.5 * x * x - 1.5 * y * y
The distortion reduces the quality of the mesh.
python.exe ../../../data/geom/mesh/utilities/vertices_map.py bend mesh.txt distorted.txt

The distorted mesh. The minimum modified condition number is 0.15; the mean is 0.61.
utility/boundary33.exe distorted.txt boundary.txt optimization/topologicalOptimize3.exe -manifold=boundary.txt -angle=0.5 distorted.txt t1.txt optimization/geometricOptimize3.exe -boundary=boundary.txt -dihedralAngle=0.5 t1.txt t1g1.txt optimization/topologicalOptimize3.exe -manifold=boundary.txt -angle=0.5 t1g1.txt t2g1.txt optimization/geometricOptimize3.exe -boundary=boundary.txt -dihedralAngle=0.5 t2g1.txt t2g2.txt optimization/topologicalOptimize3.exe -manifold=boundary.txt -angle=0.5 t2g2.txt t3g2.txt optimization/geometricOptimize3.exe -boundary=boundary.txt -dihedralAngle=0.5 t3g2.txt t3g3.txt
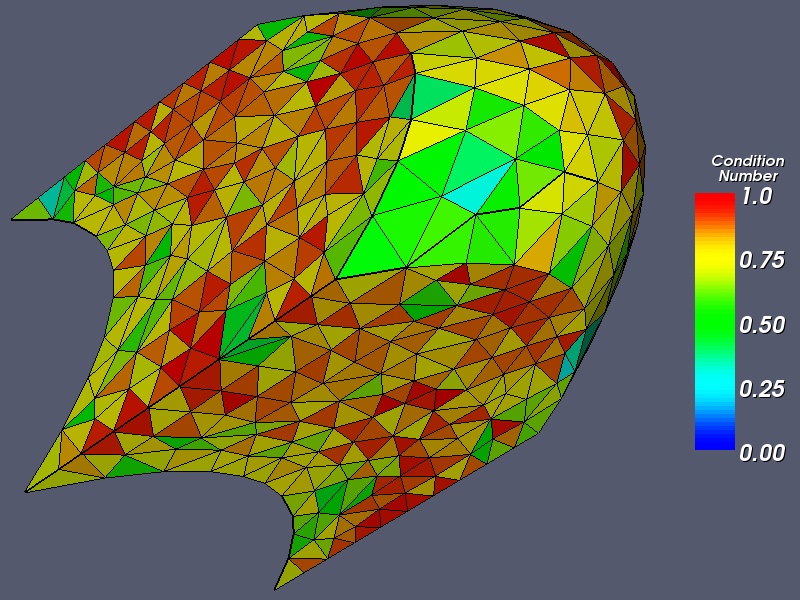
1 optimization cycle. The minimum modified condition number is 0.22; the mean is 0.79.
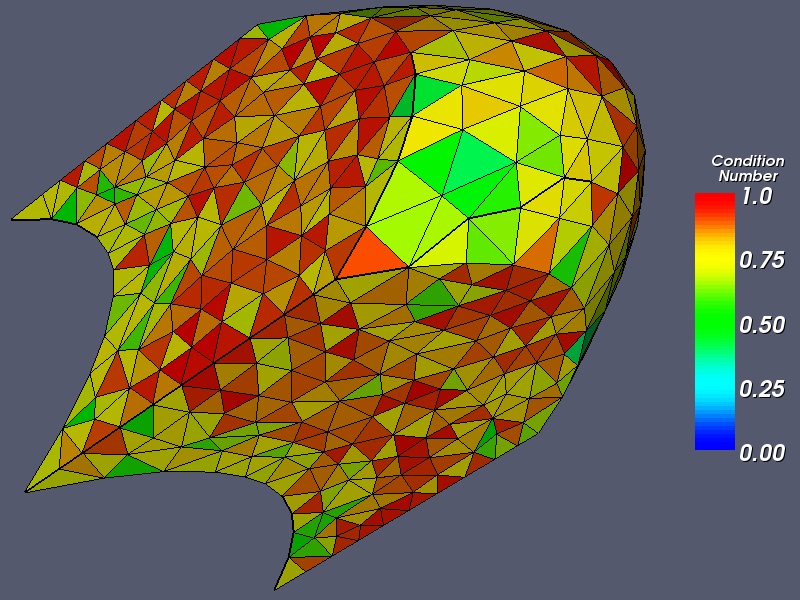
2 optimization cycles. The minimum modified condition number is 0.37; the mean is 0.82.
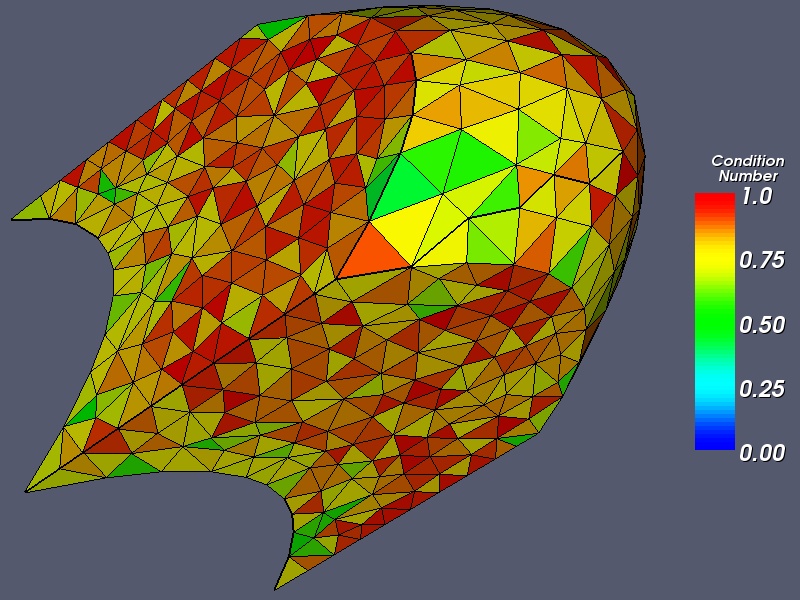
3 optimization cycles. The minimum modified condition number is 0.38; the mean is 0.84.
Generated on Thu Jun 30 02:14:57 2016 for Computational Geometry Package by
 1.6.3
1.6.3