SimplexModDet< T > Class Template Reference
Implements operations for modifying the determinant of the Jacobian. More...
#include <SimplexModDet.h>
Public Types | |
| typedef T | Number |
| The number type. | |
Static Public Member Functions | |
Mathematical functions | |
| static Number | getEpsilon () |
| Return epsilon. | |
| static Number | getDelta (const Number minDeterminant) |
| Return delta. | |
| static Number | getH (Number determinant, Number minDeterminant) |
| Return a number that is close to the determinant when it is positive and small and positive when the determinant is negative. | |
Detailed Description
template<typename T = double>
class SimplexModDet< T >
Implements operations for modifying the determinant of the Jacobian.
- Parameters:
-
T is the number type. By default it is double.
This class cannot be constructed. Its member data and public member functions are static.
The Modified Determinant
See the documentation of the geom::SimplexJac class for information on the Jacobian matrix of a simplex. When the content of a simplex vanishes, its Jacobian matrix becomes singular. That is, its determinant vanishes. This presents a problem for some algebraic quality metrics. The condition number metric and the mean ratio metric (implemented in geom::SimplexCondNum and geom::SimplexMeanRatio) become singular as the content vanishes. In order to define these metrics for simplices with vanishing and negative content, we use a modified value 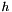 of the Jacobian determinant
of the Jacobian determinant 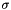 which has the following properties:
which has the following properties:
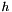 is close to
is close to 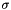 when
when 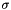 is positive and
is positive and 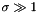 .
.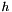 is small and positive when the determinant is negative.
is small and positive when the determinant is negative.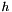 is differentiable.
is differentiable.
Let 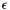 be a number that is a little bigger than the machine precision. (We use 100 times the machine precision.) Define
be a number that is a little bigger than the machine precision. (We use 100 times the machine precision.) Define
![\[ \delta = \sqrt{ \epsilon (\epsilon - \sigma) }. \]](form_227.png)
The modified value of the determinant is
![\[ h = \frac{ \sigma + \sqrt{ \sigma^2 + 4 \delta^2 } }{ 2 }. \]](form_228.png)
Usage
Consider a complex of simplices. (Perhaps the tetrahedra that are adjacent to a vertex.) Let minDeterminant be the minimum determinant of the simplices in the complex and determinant be the determinant of a given simplex. h(determinant,minDeterminant) returns the modified determinant. If the minimum determinant is no less than 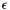 then
then h() returns the un-modified determinant.
Member Function Documentation
| static Number SimplexModDet< T >::getH | ( | Number | determinant, | |
| Number | minDeterminant | |||
| ) | [static] |
Return a number that is close to the determinant when it is positive and small and positive when the determinant is negative.
- Returns:
- Let
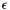 be the value of epsilon() and
be the value of epsilon() and 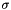 be the Jacobian determinant. Define
be the Jacobian determinant. Define
Return![\[ \delta = \sqrt{ \epsilon (\epsilon - \sigma) }. \]](form_227.png)
![\[ \frac{ \sigma + \sqrt{ \sigma^2 + 4 \delta^2 } }{ 2 }. \]](form_229.png)
The documentation for this class was generated from the following file:
Generated on Thu Jun 30 02:14:58 2016 for Computational Geometry Package by
 1.6.3
1.6.3