AMROC's beam solver - Documentation

A finite difference solver based on the equation

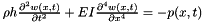
$ \rho h \frac{\partial^2 w(x,t)}{\partial t^2}+ E I \frac{\partial^4 w(x,t)}{\partial x^4} = -p(x,t) $

where I is the moment of inertia divided by the beam width, p(x,t) the pressure loading, and w(x,t) the displacement. Typical boundary conditions at both ends, such as fixed, freely moving, momentum-free, are supported. The equation is transformed into a first-order system and temporally discretized with Crank-Nicholson. A straightforward LR decomposition is used for direct solution of the set of linear equations.

Generated on Thu Jun 30 02:19:41 2016 for AMROC's Beam solver by  doxygen 1.6.3