AMROC - Adaptive Mesh Refinement in Object-oriented C++

AMROC is the fluid solver framework within the VTF software. The framework supplies a generic object-oriented implementation in C++ of the special version of the blockstructured adaptive mesh refinement algorithm of Marsha Berger and J. Oliger [1] that has been proposed by Marsha Berger and Phil Colella in [2]. This special algorithm is designed especially as a general framework for the adaptive solution of hyperbolic partial differential equations of the form:

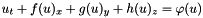
An efficient parallelization strategy for distributed memory machines has been implemented and the codes can be run on all high-performance computers that provide the MPI-library.

AMROC extends the capabilities of an arbitrary simple solution-routine for a conservative time-explicit finite-volume scheme formulated on a single uniform grid or patch to a complex multi-level simulation code. The only requirement for a seamless integration is that the numerical solution-routine returns the numerical fluxes back to the framework. The fluxes must be known (temporarily) to the framework to allow a conservative flux-correction in grid-cells that abut finer subgrids.

The core of AMROC is built on top of the Hierarchical Data Structures package. AMROC oOutput files are written in HDF4 format. Conversion into various other file formats and visualization capabilities are provided by AMROC's HDF Tools. AMROC Core and AMROC's HDF Tools use the little AMROC's Parameter IO package for processing input files.

The framework has recently been supplemented with a generic implementation of the ghost-fluid method that allows the consideration of complex imbedded boundaries in an arbitrary Cartesian method. This boundary treatment leads to a diffused numerical representation of the boundary conditions throughout the original Cartesian finite volume scheme. Complex triangulated shapes generated as ISS files by commercial meshers are considered by utilizing the Closest Point Transform package. Values in internal ghost cells are constructed with special Inter-/Extrapolation routines.

[1] M. Berger and J. Oliger. Adaptive mesh refinement for hyperbolic partial differential equations. J. Comput. Phys., 53:484-512, 1984.

[2] M. Berger and P. Colella. Local adaptive mesh refinement for shock hydrodynamics. J. Comput. Phys., 82:64-84, 1988.