Next: Initial Conditions Up: Detonations with One-Step Chemistry Previous: Detonations with One-Step Chemistry
Normalization
Under the assumption of a planar stationary detonation wave propagating with constant speed d the inhomogeneous Euler equations can be solved exactly. These planar one-dimensional solutions are used as initial conditions for all simulations with the one-step model.
Further on, all following computations for the one-step reaction model utilize dimensionless quantities. With
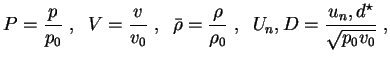
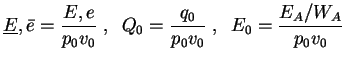
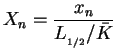 with
with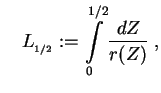
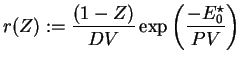 and
and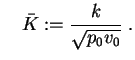
Table of Contents Home Contact